Энтропия как физическая величина
Энтропию относят к наиболее важным физическим понятиям. В качестве физической величины ее ввел Р. Клаузиус в 1865 году.
Потребность введения энтропии вызвана:
- необходимостью замены количества теплоты на некоторую функцию состояния;
- поиском параметра, который был бы сопряжен температуре, что позволило завершить этап формирования понятийного аппарата термодинамики.
Поясним пункт 2. Можно сказать, что все термодинамические параметры формируют пары (пары сопряженных величин). Например, объем и давление. Эти величины входят в определение работы:
$dA=pdV$ .
Так как количество теплоты можно записать как:
$\delta Q=TdS$,
Готовые работы на аналогичную тему
- Курсовая работа Энтропия вселенной 410 руб.
- Реферат Энтропия вселенной 270 руб.
- Контрольная работа Энтропия вселенной 240 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
то по аналогии с сказанным выше, логично предположить, что энтропия и температура являются сопряженными. В этой паре один параметр зависит от объема, например, энтропия, а температура от объема не зависит.
Энтропию вводит второе начало термодинамики. Зоммерфельд формулировал второе начало термодинамики следующим образом:
Любая система в термодинамике может быть описана функцией состояния, которую называют энтропией. Энтропию находят так:
- Систему переводят из некоторого начального состояния в избранное конечное состояние посредством череды равновесных состояний.
- Находятся все порции тепла, которые подводились в проводимых процессах ($\delta Q$).
- Данные порции тепла делятся на абсолютную температуру ($T$).
- Полученные отношения складываются.
При необратимых процессах энтропия замкнутой системы увеличивается.
Так, энтропию, а вернее ее изменение, для обратимого процесса, можно определить следующим образом:
Определение 1
Изменение энтропии в обратимом процессе равно:
$\Delta S=\sum\limits_i {\frac{\Delta Q_{i}}{T_{i}}\left( 1 \right).} $
Для непрерывного процесса:
$\Delta S=\int\limits_a^b {\frac{\delta Q}{T}\left( 2 \right).} $
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут!
Задать вопрос
Замечание 1
Второе начало термодинамики осуществляет ввод энтропии формально, как некоторую функцию состояния, при этом физический смысл энтропии не раскрывается.
Термодинамика не в состоянии установить связь энтропии с внутренним состоянием и молекулярными свойствами исследуемой системы, и не может показать способ установления данной связи.
Свойства и физический смысл энтропии раскрывает статистическая физика, когда рассматривает микросостояния вещества. Л. Больцман первым предположил, что термодинамическая вероятность связана с энтропией. Это предположение в виде формулы записал Планк:
$S=k ln(W) (3),$
где $k$ – постоянная Больцмана; $W$ – термодинамическая вероятность (число способов реализации макросостояния при помощи микросостояний).
Смысл энтропии в том, что она является мерой беспорядка в термодинамической системе. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
Просто о сложном: почему все вокруг стремится к хаосу и как это остановить
Когда порой вы чувствуете нарастающий уровень энтропии, но не понимаете почему, ответ кроется в физике: стремление мира к хаосу — фундаментальное свойство природы. Из чего состоит хаос, обратим ли он, можно ли его как-то измерить и почему существует выражение «ломать — не строить»? Обо всем этом T&P рассказал научный журналист, сотрудник кафедры физики и астрофизики МФТИ Айк Акопян в рамках проекта «Физтех.Читалка».
Айк Акопян
Что происходит, когда мы приводим в движение маятник? Он начинает колебаться, каждый раз уменьшая амплитуду. Через некоторое время мы обнаружим, что маятник остановился. Но куда делась энергия маятника? Те, кто в школе на уроках физики слушал учителя внимательно, ответят, что энергию заберут молекулы воздуха. Но почему не происходит обратное? Почему молекулы вдруг не могут собраться и, наоборот, передать энергию маятнику?
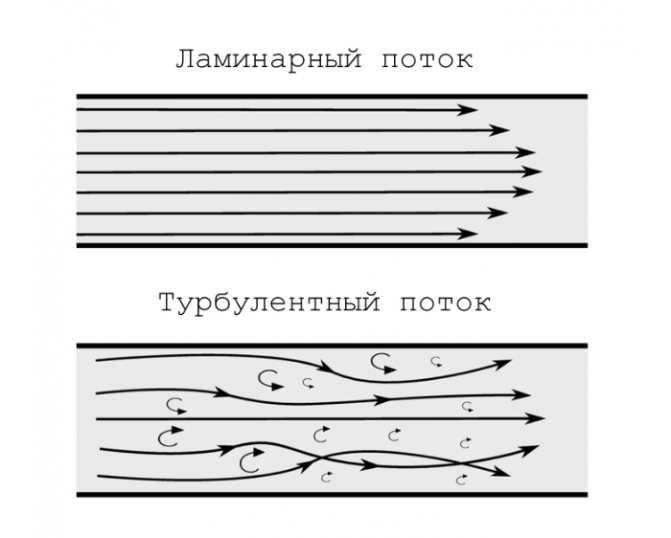
Дело в том, что стремление мира к хаосу оказывается фундаментальным свойством природы. Направленное движение частиц маятника превращается в хаотичное движение молекул воздуха. Направленное течение воды рано или поздно превратится в хаотичную струю с турбулентными вихрями и извивающимися, переплетающимися друг с другом потоками.
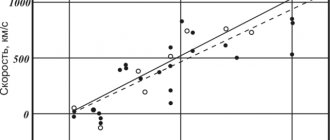
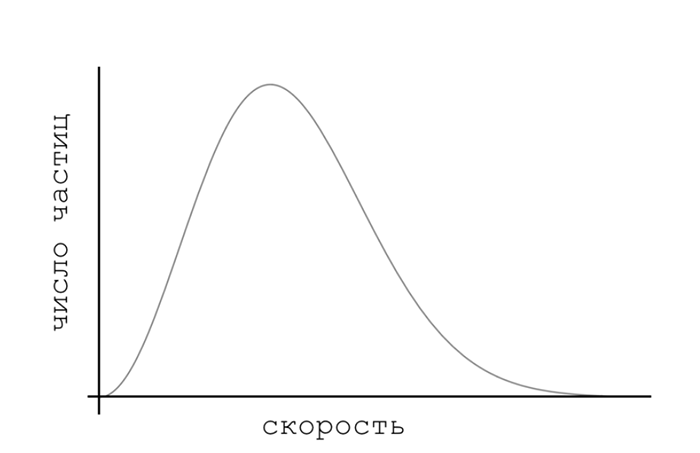
Наша природа вовсю стремится к хаосу, но неужели это стремление бесконечно? В какой момент система достигает какого-то спокойствия? В какой момент это стремление прекращается? В XIX веке Максвелл и ряд других физиков показали, что, если оставить систему в покое, она действительно придет к определенному состоянию «спокойствия». Это состояние называется равновесным, и, чтобы его понять, нужно забыть об индивидуальной скорости, координате каждой частицы и взглянуть на какие-то коллективные характеристики системы. Например, на то, сколько частиц на данный момент имеют определенные скорости.
Если мы построим график числа частиц от скорости, то увидим удивительную вещь: система из любого состояния, каким бы это состояние ни было изначально, в итоге приходит к одному определенному распределению числа частиц от скорости, которое называется распределением Максвелла. Это состояние является конечным пунктом назначения любой системы, и в ней достигается максимальный хаос.

Но… Как вообще измерить хаос? В физике для измерения хаоса используют величину, которая называется энтропией системы. Чем больше энтропия, тем менее упорядочена система. В состоянии равновесия энтропия максимальна. Больцманом в XIX веке была доказана так называемая H-теорема, которая гласит, что в замкнутой системе энтропия со временем всегда возрастает.


На практике это несет за собой вполне понятные последствия. Если мы, например, возьмем шарик с гелием и взорвем его в углу комнаты, то газ через некоторое время разлетится по всей комнате, заполнив равномерно ее всю. Таким образом, энтропия газа увеличится до максимума и… Да, в общем-то, и все. Сколько бы мы ни ждали, гелий никогда не соберется обратно в кучу в углу комнаты. То есть процессы в нашем мире необратимы: из конечного состояния мы никак не можем узнать начальное, так как конечное состояние одинаково для всех начальных состояний. Это вполне понятно, наш опыт вполне этому соответствует. Всегда легче что-то сломать, чем построить, легче разбросать, чем собрать воедино. Это все вполне логично, так?
Не совсем. Представьте, что у вас есть замкнутая комната с кучей шариков, которые летят и врезаются друг в друга. Все абсолютно идеально, столкновения упругие, никаких потерь энергии. Через достаточное количество времени распределение скоростей будет в точности максвелловским, энтропия необратимо возрастет до максимума.
Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы
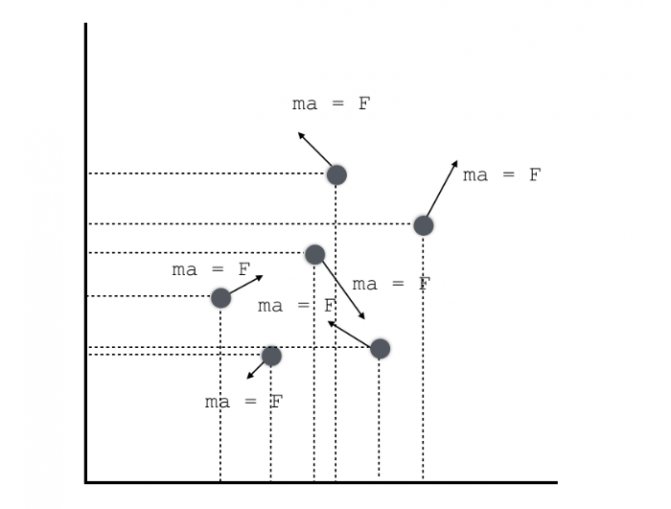
Но давайте взглянем на каждый шарик по отдельности. Дело в том, что для каждого шарика мы можем узнать в точности его скорость и координату, а также действующую на него силу. Из второго закона Ньютона можем узнать ускорение — и все: движение каждой отдельной частички можно совершенно однозначно задать. Закон Ньютона по времени обратим, так как, если повернуть время вспять, свою форму закон не изменит. Это означает, что и движение каждого отдельного шарика тоже обратимо: из конечного состояния шарика можно понять, откуда он пришел и как двигался, но… Но движение всех шариков вместе оказывается необратимым.

То есть в основе нашего необратимого мира лежат вполне себе обратимые законы. Это весьма странно. А что, если никакой необратимости нет, а это всего лишь иллюзия? Что, если движение просто настолько сложное, что оно кажется нам хаотичным, а на самом деле оно вполне регулярно?
Для примера того, что имеется в виду, возьмем очень интересную систему. Она называется клеточный автомат. Представьте, что ваша Вселенная — это простой ряд из белых и черных клеточек. Вы — бог этой Вселенной, и вам нужно заложить какое-то правило эволюции по времени. И вы закладываете очень простое правило: если сама клетка черная и соседние две клетки тоже черные, то в следующем шаге клетка будет белой (на картинке снизу слева), если клетка черная, сосед слева тоже черный, а сосед справа белый, то в следующем шаге клетка станет черной и так далее. Таким образом можно задать универсальное правило (физику) вашей Вселенной. Записать этот закон можно с помощью нулей и единичек или, если перевести их в десятиричную запись, с помощью просто одного числа. В данном случае (на картинке) это будет правило 90. Эволюция такого клеточного автомата показана ниже.


Таких правил существует очень много. Есть правила, которые опираются на два предыдущих шага вместо одного или на нескольких соседей. Есть правила для двумерного клеточного автомата, где у нас теперь не ряд из черных и белых клеточек, а целая плоскость.
С помощью клеточных автоматов уже получают совершенно сложные, непредсказуемые фигуры — их используют в архитектуре и игровом дизайне для построения реалистичного ландшафта. Но, что удивительно, все это разнообразие, эти непредсказуемые формы и образы задаются всего лишь правилом из одного числа, все остальное — дело времени.


Но что, если все разнообразие нашего мира, все сложные образы, создаваемые нашей природой, и весь тот хаос, к которому стремится наш мир, — это всего лишь реализация какого-то клеточного автомата? Что, если мы просто являемся симуляцией клеточного автомата в чьем-нибудь компьютере?
Как мы поняли в первой части, в самой глубокой основе нашего мира лежат вполне обратимые законы, где по конечному состоянию можно восстановить начальное. Поэтому если мир и есть клеточный автомат, то он должен также быть обратимым. Такие клеточные автоматы действительно есть, но у них есть одна проблема. У любого обратимого клеточного автомата есть цикл: через определенное число шагов Вселенная воссоздается в своем первоначальном виде снова, затем снова — и движется так по циклу.
В нашем мире, к сожалению, такого нет… Или есть? Французский математик Анри Пуанкаре для определенного типа систем заметил интересную вещь: в результате эволюции этих систем со временем они возвращались в свое первоначальное состояние, хотя изначально казалось, что стремятся они лишь в сторону хаоса. Такой цикл назвали циклом Пуанкаре.


Напрашивается очень интересная мысль. Да, действительно, газ из взорвавшегося гелиевого шарика в одну кучу обратно не соберется, но что, если подождать еще дольше? Что, если цикл Пуанкаре для такой системы очень большой? Есть целые космологические модели, основанные на гипотезе возврата Пуанкаре, одна из них принадлежит известному математику Пенроузу. По его мнению, Вселенная сначала раздувается, затем схлопывается обратно, затем снова взрывается, раздувается и вновь схлопывается, повторяя в точности предыдущий цикл.
Но у такой теории циклической Вселенной есть большой минус: мы пока не знаем процессов, способных заставить Вселенную схлопнуться. Где их искать? Так ли хорошо мы знаем нашу Вселенную? Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы. Мы с грехом пополам знаем лишь о 2% нашей Вселенной, а об остальных 98% не знаем вообще ничего. То есть если представить, что наша Вселенная — это большой прекрасный замок с башнями, мостами, тронными залами и прочим, то из подвала мы пока не выходили, и кто знает, какие тайны ждут нас там, наверху.
Теория тепловой смерти Вселенной
Р. Клаузиус второе начало термодинамики сформулировал следующим образом:
- энергия Мира является неизменной;
- при этом энтропия Мира стремится к максимуму.
Данная формулировка означает то, что Вселенная стремится в состояние термодинамического равновесия (это состояние названо тепловой смертью), этому состоянию соответствует полный хаос в системе.
Представление Клаузиуса о тепловой смерти Вселенной несостоятельно, так как в этой области законы термодинамики не работают. Термодинамические положения применимы к термодинамическим системам. Один из признаков такой системы – это аддитивность некоторых ее параметров, например, энергии. Так, при разбиении системы, находящейся в состоянии равновесия на отдельные равновесные макроскопические части, энергию всей системы можно найти как сумму энергий ее частей. При этом энергия системы будет пропорциональна ее объему.
Данного признака у Вселенной нет, поскольку ее гравитационная энергия не является пропорциональной объему, так как силы гравитации дальнодействующие и неэкранируемые. Суммарная энергия Вселенной опять же не пропорциональна объему и в этой связи, не аддитивна. Еще следует заметить, что Вселенная не пребывает в стационарном состоянии, происходит ее расширение. Из сказанного сделаем вывод о том, что говорить об энтропии Вселенной в термодинамическом смысле нельзя, так как Вселенная — это не термодинамическая система.
Закон сохранения энтропии во Вселенной[ | ]
В общем случае, приращение внутренней энергии имеет вид:
d E = T d S − p d V + ∑ i μ i d N i . {\displaystyle dE=TdS-pdV+\sum \limits _{i}\mu _{i}dN_{i}.}
Учтем, что химический потенциал частиц и античастиц равны по значению и противоположны по знаку:[уточнить
]
d E = T d S − p d V + ∑ i μ i ( d N i − d N ¯ i ) . {\displaystyle dE=TdS-pdV+\sum \limits _{i}\mu _{i}(dN_{i}-d{\overline {N}}_{i}).}
Если считать расширение равновесным процессом, то последние выражение можно применить к сопутствующему объёму ( V ∝ a 3 {\displaystyle V\propto a^{3}} , где a {\displaystyle a} — «радиус» Вселенной). Однако, в сопутствующем объёме разница частиц и античастиц сохраняется. Учитывая этот факт, имеем:
T d S = ( p + ρ ) d V + V d ρ . {\displaystyle TdS=(p+\rho )dV+Vd\rho .}
Но причиной изменения объёма является расширение. Если теперь, учитывая это обстоятельство, продифференцировать по времени последнее выражение:
T d S d t = a 3 [ 3 a ˙ a ( p + ρ ) + ρ ˙ ] . {\displaystyle T{\frac {dS}{dt}}=a^{3}\left[3{\frac {\dot {a}}{a}}(p+\rho )+{\dot {\rho }}\right].}
Теперь, если подставить уравнение неразрывности, входящую в систему уравнений Фридмана:
T d S d t = 0. {\displaystyle T{\frac {dS}{dt}}=0.}
Последнее означает, что энтропия в сопутствующем объёме сохраняется.
Энтропия объектов Вселенной
Энтропией Вселенной считают величину, определяющую степень беспорядка и ее тепловое состояние.
Во Вселенной можно выделять подсистемы, которые можно описывать как термодинамические системы, например:
- такие компактные объекты, как звезды, планеты и т.д.;
- реликтовое излучение (тепловое излучение температура которого составляет 2,73 К).
Сделанные вычисления показали, что суммарная энтропия всех компактных объектов, которые смогли наблюдать, очень маленькая, если сравнить ее с энтропией реликтового излучения. Причиной этому может служить то, что количество реликтовых фотонов огромно. Каждому атому во Вселенной соответствует $10^9$ фотонов.
Современные оценки суммарной энтропии доли Вселенной, доступной для исследования, дают величину порядка $10^{90} k$. Сравним эту цифру с энтропией вещества черной дыры такой же части Вселенной, которая составит $10^{124} k$. Эти цифры говорят о том, что наша часть Вселенной далека от максимально неупорядоченного состояния.