Из истории гравитационной постоянной
Интересно, что в работах Ньютона нет такой величины. Она появилась в физике существенно позже. Если быть конкретнее, то только в начале девятнадцатого века. Но это не значит, что ее не было. Просто ученые ее не определили и не узнали ее точное значение. Кстати, о значении. Гравитационная постоянная постоянно уточняется, поскольку является десятичной дробью с большим количеством цифр после запятой, перед которой стоит ноль.
Именно тем, что эта величина принимает такое маленькое значение, объясняется то, что действие сил гравитации незаметно на небольших телах. Просто из-за этого множителя сила притяжения оказывается ничтожно маленькой.
Впервые опытным путем установил значение, которое принимает гравитационная постоянная, физик Г. Кавендиш. И случилось это в 1788 году.

В его опытах использовался тонкий стержень. Он был подвешен на тоненькой проволоке из меди и имел длину около 2 метров. К концам этого стержня были прикреплены два одинаковых свинцовых шара диаметром 5 см. Рядом с ними были установлены большие свинцовые шары. Их диаметр был уже 20 см.
При сближении больших и маленьких шаров наблюдался поворот стержня. Это говорило об их притяжении. По известным массам и расстоянию, а также измеренной силе закручивания удалось достаточно точно узнать, чему равно гравитационное постоянное.
Эксперимент Кавендиша
Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».


Генри Кавендиш (1731 — 1810)
Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.


Установка Генри Кавендиша
Более наглядное описание эксперимента доступно в видео ниже:
Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли. Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.
А Вы смотрели: Специальная теория относительности
А началось все со свободного падения тел
Если поместить в пустоту тела разной массы, то они упадут одновременно. При условии их падения с одинаковой высоты и его начала в один и тот же момент времени. Удалось рассчитать ускорение, с которым все тела падают на Землю. Оно оказалось приблизительно равно 9,8 м/с2.
Ученые установили, что сила, с которой все притягивается к Земле, присутствует всегда. Причем это не зависит от высоты, на которую перемещается тело. Один метр, километр или сотни километров. Как бы далеко ни находилось тело, оно будет притягиваться к Земле. Другой вопрос в том, как ее значение будет зависеть от расстояния?
Именно на этот вопрос нашел ответ английский физик И. Ньютон.
Гравитация Земли
Солнечная система > Система Земля-Луна > Планета Земля > Гравитация Земли
Гравитационная карта Земли. Красные участки: области повышенной гравитации
Сила гравитации и гравитационное поле Земли. Узнайте точное значение гравитации на экваторе и полюсах планеты, влияние массы, вращения Земли на силу притяжения.
Если бы не гравитация Земли, нас бы всех унесло в космос. Так что не паникуйте, когда я сообщу, что скорость вашего падения по мере приближения к Земле увеличивается до 9.8 м/сек2. К счастью, вас спасает то, что вы находитесь на поверхности планеты. Можете посмотреть на карту, где показана сила притяжения Земли.
Гравитация зависит от массы. Чем больше масса объекта, тем с большей силой гравитация влияет на объекты вокруг него. Сила притяжения Земли, которую вы испытываете при падении, зависит от расстояния. Так, сила притяжения, которую вы ощущаете на поверхности Земли значительно отличается от той, которую бы вы испытывали, находясь на расстоянии до Луны, или еще дальше. На поверхности планеты сила притяжения составляет 9,8 м/с2.
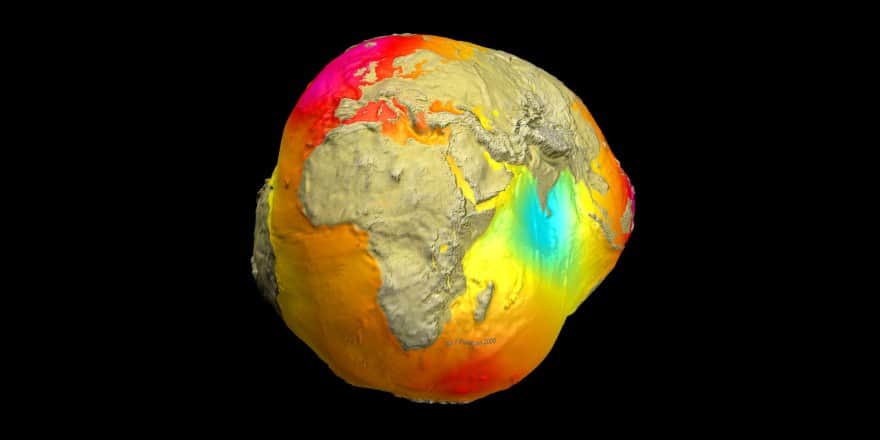

Гравитационная 3D модель Земли
Вы будете удивлены, узнав, что гравитация на Земле меняется в зависимости от того, в какой ее точке вы находитесь. Первая причина — это вращение Земли. Это вращение затягивает вас в космос, но не волнуйтесь, его силы недостаточно. Сила притяжения Земли на экваторе составляет 9.789 м/с2, а на полюсах 9.832 м/с2. Другими словами, ваш вес на полюсах больше, чем на экваторе, из-за центробежной силы.
С увеличением высоты сила земной гравитации уменьшается, так как увеличивается расстояние от центра Земли. При восхождении на гору она достигает минимального значения (на вершине Эвереста сила притяжения уменьшиться 0.28%), но если вы поднимитесь на высоту Международной космической станции, то сила притяжения составит 90 процентов.
Наконец, сила притяжения зависит от того, что находится под вами. Высокая плотность пород меняет силу гравитации, которую вы можете почувствовать, хотя ее величина очень незначительная. В НАСА уже вычислили силу гравитационного поля Земли с невероятной точностью.
Сегодня написано много статьей на тему Земли во Вселенной. Здесь вы можете ознакомиться с полной гравитационной картой нашей планеты.
Уменьшение силы притяжения тел с их отдалением
Для начала он выдвинул предположение о том, что сила тяжести убывает. И ее значение находится в обратной зависимости от расстояния, возведенного в квадрат. Причем это расстояние нужно отсчитывать от центра планеты. И провел теоретические расчеты.

Потом этот ученый воспользовался данными астрономов о движении естественного спутника Земли — Луны. Ньютон рассчитал, с каким ускорением она вращается вокруг планеты, и получил те же результаты. Это свидетельствовало о правдивости его рассуждений и позволило сформулировать закон всемирного тяготения. Гравитационная постоянная в его формуле пока отсутствовала. На этом этапе было важно определить зависимость. Что и было сделано. Сила тяжести уменьшается обратно пропорционально расстоянию от центра планеты, возведенному в квадрат.
Работы Ньютона
Примечательно, что в трудах Ньютона (1684—1686) гравитационная постоянная в явном виде отсутствовала, как и в записях других ученых аж до конца XVIII-го века.


Исаак Ньютон (1643 — 1727)
Ранее использовался так называемый гравитационный параметр, который равнялся произведению гравитационной постоянной на массу тела. Нахождение такого параметра в то время было более доступно, поэтому на сегодняшний день значение гравитационного параметра различных космических тел (в основном Солнечной системы) более точно известно, нежели порознь значение гравитационной постоянной и массы тела.
µ = GM
Здесь: µ — гравитационный параметр, G – гравитационная постоянная, а M — масса объекта.
А Вы смотрели: Черная дыра в космосе: откуда она возникает
Размерность гравитационного параметра — м3с−2.
Следует отметить тот факт, что значение гравитационной постоянной несколько варьируется даже до сегодняшнего дня, а чистое значение масс космических тел в то время было определить довольно сложно, поэтому гравитационный параметр нашел более широкое применение.
К закону о всемирном тяготении
Ньютон продолжил размышления. Поскольку Земля притягивает Луну, то и она сама должна притягиваться к Солнцу. Причем сила такого притяжения тоже должна подчиняться описанному им закону. А потом Ньютон распространил его на все тела вселенной. Поэтому и название закона включает слово «всемирное».
Силы всемирного тяготения тел определяются как пропорционально зависящие от произведения масс и обратные квадрату расстояния. Позже, когда был определен коэффициент, формула закона приобрела такой вид:
- Fт = G (m1 *х m2) : r2.
В ней введены такие обозначения:
| Сила тяготения | Fт |
| Гравитационная постоянная | G |
| Массы тел | m1, m2 |
| Расстояние между телами | r |
Формула гравитационной постоянной вытекает из этого закона:
- G = (Fт Х r2) : (m1 х m2).
Ссылки
- Гравитационная постоянная // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Милюков В. К.
Гравитационная постоянная // Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 523. - Speake C., Quinn T.
The search for Newton’s constant // Physics Today. — 2014. — Vol. 67, № 7. — P. 27—33. - Иванов И.
Гравитационная постоянная измерена новыми методами // Элементы. — 22.01.2007. - Измерение гравитационной постоянной (большой G) как повод для дебатов!
Значение гравитационной постоянной
Теперь настал черед конкретных чисел. Поскольку ученые постоянно уточняют это значение, то в разные годы были официально приняты разные числа. К примеру, по данным за 2008 год гравитационная постоянная равна 6,6742 х 10-11 Нˑм2/кг2. Прошло три года — и константу пересчитали. Теперь гравитационная постоянная равна 6,6738 х 10-11 Нˑм2/кг2. Но для школьников в решении задач допустимо ее округление до такой величины: 6,67 х 10-11 Нˑм2/кг2.
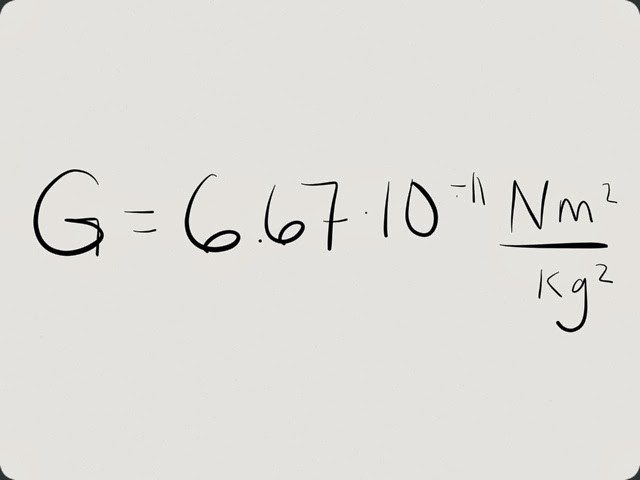
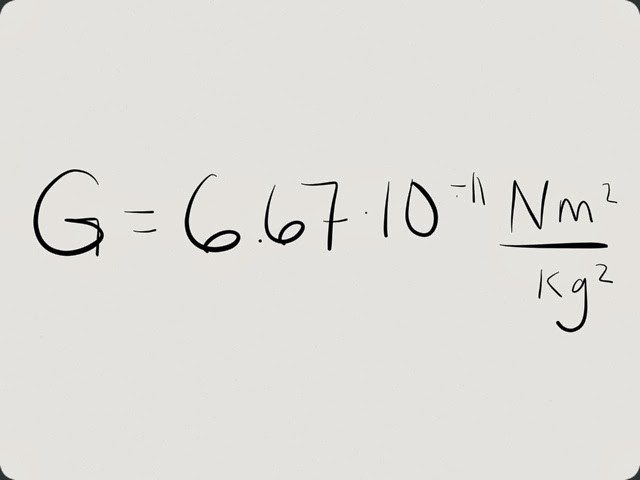
Солнечная система состоит из планет с их спутниками, астероидов, комет, мелких метеорных тел, космической пыли. Законы движения и происхождения всех этих тел неразрывно связаны с центральным объектом системы — Солнцем. Основной силой, управляющей движением планет и связывающей воедино Солнечную систему, является электрическая сила Солнца. При этом для тел Солнечной системы характерны два признака.
Во-первых, тело за счет своей кинетической энергии не может преодолеть силы солнечного притяжения и покинуть Солнечную систему.
Во-вторых, тело, принадлежащее Солнечной системе, должно постоянно находиться в области преобладающего притяжения Солнца.
Заметим, что для всех планет с их спутниками, астероидов, практически всех комет, находящихся в сфере действия Солнца, оба условия выполняются. Данные об орбитах и некоторых физических свойствах планет, являющихся главными членами Солнечной системы, приведены в таблице 3.1.
Все планеты обращаются вокруг Солнца в одной и той же плоскости, примерно совпадающей с плоскостью солнечного экватора, и движутся в одинаковом направлении, совпадающем с направлением осевого вращения Солнца (против часовой стрелки, если смотреть на Солнечную систему с северного полюса мира).
Однако имеется очень большая диспропорция в распределении массы и момента количества движения между Солнцем и планетами, если определить эти парамет -ры по известному «закону тяготения Ньютона». Так, по этому закону удельный (на единицу массы) момент количества движения у планет больше, чем у Солнца, в среднем в 35 • 103 раз [24]. В соответствии с изложенными выше признаками для существования Солнечной системы такое отклонение от закона движения должно было привести к ее разрушению. Это обстоятельство является непреодолимым препятствием для нынешней физики, хотя были попытки объяснить такое нарушение закона сохранения момента количества движения с привлечением магнитогидродинамики [24].
Фрактальная физика позволяет разрешить эту проблему и определить реальные параметры планет [2]. Автором установлен глобальный закон всеобщего взаимодействия (сформулирован в п. 3.1) и, как следствие, определен локальный закон тяготения. Сущность локального закона тяготения заключается в том, что взаимодействие заряженных масс веществ во Вселенной осуществляется электромагнитной силой через тонкую
структуру пространства. Гравитационное взаимодействие является различимым эффектом единого фундаментального электромагнитного взаимодействия.
Выявлено (см. п. 3.1), что Солнце — это звезда, имеющая положительный электрический заряд, равный + 3,3 • 1014Кл. Электрический отрицательный заряд планет создается как методом электростатической индукции звезды, так и ионизацией атомов или молекул веществ планет, вызываемой поглощением квантов электромагнитного излучения Солнца. Заметим, что энергия квантов не зависит от расстояния, однако с увеличением расстояния уменьшается число (плотность) частиц света. В таблице 3.1 представлены результаты расчетов с учетом установленного механизма создания заряда планет. Заряд Земли -5,7 • 105Кл создается электростатической индукцией Солнца, ибо озоновый слой ее атмосферы не пропускает рентгеновское излучение. Однако рентгеновское излучение является основным источником создания заряда планет группы Юпитера, ибо действие в создании заряда этих планет методом электростатической индукции незначительно. Электростатическая индукция определяет в этом случае направление (знак) ионизации. Поэтому Землю (и другие планеты), по аналогии с прохождением света через линзу, следует рассматривать как электрическую линзу, а не источник электрического поля. Непонимание данного явления привело к величайшему заблуждению нынешней физики относительно природы гравитации (тяготения). Ведь воздействие отрицательного заряда Земли происходит в большей частью положительно заряженной атмосфере, поэтому напряженность электрического поля Земли быстро падает по мере удаления от нее. Причина этого в том, что положительный заряд атмосферы компенсирует только в локальных областях влияние отрицательного заряда Земли, вызванного положительным зарядом Солнца +3,3 • 1014 Кл. Однако глобальное и практически мгновенное воздействие заряда Земли через структуру
пространства в принципе бесконечно, что подтверждается движением со скоростью 1,03 км/с положительно заряженной Луны, обращающейся вокруг планеты на расстоянии 384,4 • 106 м. Движение Луны вызывается зарядом Земли -5,7 • 105 Кл (см. п. 2.5).
Кроме того, отметим, в связи с разрушением Земли и озонового слоя ядерными взрывами и запусками ракет электрическое поле у земной поверхности (средний вертикальный градиент электрического потенциала) изменилось и составляет около 150 В/м; напомним: ранее среднее электрическое поле Земли составляло около 130 В/м (см. табл. 3.1). Это обусловливает изменение параметров орбитального движения Земли и, как следствие, приведет к глобальному изменению климата и потере атмосферы. Такой процесс подтверждается наблюдениями: за последние двадцать лет атмосфера Земли потеряла 20 мм своего давления, а мощность гамма-излучения в летний солнечный день 1998 г. в Москве составила утром 13, к полудню 26 мкР/ч. Геофизическая спутниковая система (см. далее) зафиксировала увеличивающее уско -рение движения Земли по орбите. В ближайшее время ускорение обращения составит 0,01 секунды. В соответствии с формулой (3.2), такое изменение периода обращения определяет уменьшение радиуса орбиты планеты на 3,6 млн. км, можно сказать, блуждание планеты до такой величины.
Геофизическая спутниковая система представляет собой три пояса космических аппаратов, разнесенных на 120° и расположенных на высоте 20 тыс. км. Один из поясов ориентирован в направлении галактического центра. Это позволяет контролировать различные изменения магнитного поля центра Галактики, электрического и магнитного полей Земли, ее озоновый слой, активность Солнца и т. д. Основным датчиком информации является кварцевый резонатор. Измерения проводятся путем сравнения бортовых данных с наземным эталоном.
Благодаря такой геофизической системе зарегистрировано не только ускорение обращения Земли по орбите, но и замедление вращения вокруг оси на 0,001 секунды. Изменение ротационного режима Земли связано с увеличением силы электрического взаимодействия планеты с Солнцем в результате разрушения озонового слоя. Данная спутниковая система позволила еще раз представить тяготение и электричество как две разные формы одной и той же сущности [94, 95].
Хотя в первом приближении мы говорим о стационарных электрических и магнитных полях объектов взаимодействия, измерения геофизической спутниковой системы зафиксировали частоты гравитационного взаимодействия в диапазоне 10-6 — 10-12 Гц [97, 98]. Солнце воспринимает гравитационное воздействие в диапазоне 0,2 — 0,6 нГц, а само излучает 5 — 6 нГц, гравитационное излучение галактического центра составляет 0,3 — 0,5 нГц. Отсюда можно увидеть, что частота Солнца 0,6 нГц есть частота гравитационного воздействия галактического центра, которая характеризует примерно 22-летнюю солнечную активность и период вращения газового диска Галактики (см. ранее п. 3.6). Теперь становится понятным, с учетом знаний по радиотехнике (см. п. 6.3), что приближенная частота магнитного взаимодействия равна единице, разделенной на удвоенный период вращения заряженного центрального объекта. Частоту fM магнитного воздействия центральных объектов представим в форме:
| (3.21) |
| — период вращения центрального объекта. |
В связи с различием электрических и магнитных полей, а также разных форм — диска и сферы — центров тяготения приближенная частота электрического взаимодействия равна единице, разделенной на произведение удвоенного периода вращения заряженного цен-
трального объекта на 4 2. Частоту £э электрического взаимодействия представим в форме:
Так как период осевого вращения Солнца составляет примерно t = 0,25 • 107с, то частота его электрического излучения, в соответствии с (3.22), составляет примерно 5 нГц, что подтверждается вышеуказанным экспериментом. Как видим, соотношения (3.21) и (3.22) открыли для нас еще одно свойство гравитационного взаимодействия.
Колебания магнитных и электрических полей следует рассматривать в виде фона, накладываемого на их стационарные составляющие. Амплитуда этого фона зависит от распределения электрического тока газового диска Галактики, а для гравитационных излучаемых колебаний Солнца — от поверхностного распределения его электрического заряда. Следует подчеркнуть значение этого фона (см. п. 3.6): если магнитное поле на поверхности Солнца изменится всего лишь на 10-5 Гс за счет колебания магнитного поля черной дыры, это вызывает изменение магнитодвижущей силы, пропорциональной радиусу звезды. Возникающая сила определяет быстрые изменения магнитных полей Солнца и движение плазмы, наподобие приливного гравитационного притяжения (см. далее п. 3.10). Мы знаем, что такие процессы на звезде оказывают влияние на нашу жизнь. При этом заметим, что частота гравитационного взаимодействия нашей электрической планеты, исходя из 24-часового периода осевого вращения, составляет примерно 1,5 • 10-7 Гц (см. соотношение (3.22)).
Кроме того, понимая сущность тяготения, мы должны отметить, что дополнительным контролем гравитационного состояния планеты должны быть измерения ускорения свободного падения во многих точках Земли.
Способ измерения тяготения должен соответствовать электромагнитной сущности природы (см. п. 3.5).
Исходя из установленного закона гравитации, автор произвел расчет масс планет. Масса М планет определяется величинами заряда q, электрического поля Е, радиуса орбиты R, скорости движения по орбите V, нормирующих коэффициентов 0 = 1/( • 109) Ф/м, , определяющих заряженную сферу планет в соответствии с законом взаимосвязи формы и энергии (см.пп. 2.5, 3.1), и выражается формулами (3.18) и (3.19) в системе СИ:
(3.23)
Расчеты по определению параметров планет, Луны и Солнца сведены в таблицу 3.2. Масса Солнца определена, исходя из магнитной связи звезды с центром Галактики, по формуле (3.15). Проведем анализ полученных результатов в сравнении с данными нынешней физики [24]: «Сила притяжения Солнца, удерживающая Землю на орбите, составляет примерно 3,6 • 1021кг. Она могла бы разорвать стальной трос диаметром в 3000 км».
Действительный закон гравитации (3.1) показывает значительно меньшее взаимодействие, а именно: сила, удерживающая Землю как заряженную сферу (а не точку) на орбите, в соответствии с формулой (3.18) F = • qE/ 0, равна 3 • 1019 Н = 3 • 1018 кгс. Видим, что ошибка нынешней физики в определении этого взаимодействия составляет 1,2 • 103 раз. Масса Земли, представленная нынешней физикой, составляет 6,0 • 1024 кг. Расчет фрактальной физики по формуле (3.23) показывает (см. табл. 3,2), что масса Земли составляет 4,9 • 1021 кг. Ошибка в определении массы Земли составляет 1,2 • 103 раз. Так как планет девять, ошибка нынешней физики в определении приведенной массы Солнечной системы составляет примерно 11 • 103 раз.
Таблица 3.2. Планеты солнечной системы
| Радиус орбиты R, а.е. | Заряд планет q, Кл | Электрическое поле Е,В/м | Скорость по орбите V, км/с | Масса планет М, кг | Плотность кг/м3 |
| Меркурий | 0,38 | -1,4-.105 | 47,0 | 0,3. 1021 | 5,2 |
| Венера | 0,72 | -6,2 .105 | 34,9 | 3,3. 1021 | 3,6 |
| Земля | 1,0 | -5,7.105 | 29,7 | 4,9. 1021 | 4,5 |
| Марс | 1,52 | -1,35.105 | 24,0 | 2,2. 1021 | 13,6 |
| Юпитер | 5,2 | -32,2.106 | 13,1 | 3,. 1024 | 2,2 |
| Сатурн | 9,5 | -17,0.106 | 9,6 | 4,4. 1024 | 4,8 |
| Уран | 19,2 | -21,2.105 | 6,8 | 1,6. 1024 | 23,5 |
| Нептун | 30,0 | -15,5. 105 | 5,4 | 2,2. 1024 | 36,4 |
| Плутон | 39,5 | -0.3.104 | 4,7 | 6,7. 1021 | 1132,6 |
1.Радиус орбиты Земли составляет 149,6 • 106км.
2. Масса Солнца 1,6 • 1030 кг, плотность 1158 кг/м3. Масса Солнца определена по формуле М = qRB/((4 )1/2), исходя из обращения звезды вокруг ядра Галактики. Данные о Солнце традиционной физики: М = 2 • 1030 кг, плотность 1410 кг/м3.
3. Масса Луны 2,2 • 1019 кг, исходя из формулы вычисления масс планет. Ошибка современной физики в определении массы Луны составляет 3 • 103 раз.
Вспомним при этом, что приведенная масса в данном случае характеризует распределение массы движущейся системы в зависимости от ее общего центра инерции — Солнца.
Установленные фрактальной физикой реальные массы
планет показывают, что закон сохранения момента
количества движения Солнечной системы выполня-
ется c точностью до нормирующего коэффициента Ö4p.
| . Этот |
Этот коэффициент обусловлен рационализацией закона Кулона [57]. Полученные результаты также указывают на существенное различие строения планет по сравнению с представлениями нынешней физики. Наличие ядра планет является вымыслом. Так, плотность Земли нынешняя физика определила в 5520 кг/м3, т. е. как плотность сплошной металлической среды [24]. Эксперименты показывают обратное: Земля состоит из отдельных частичек, она очень рыхлая, причем большие объемы ее занимают газы. Средняя плотность планеты в действительности составляет 4,5 кг/м3. Исходя из представленных результатов, в центре планет имеется пустота, заполненная газовой плазмой. Толщина оболочки Земли составляет меньше 80 км. Действительно, толщина оболочки определяется по задержке отраженного радиосигнала от пограничного расплавленного слоя, расположенного между корой и газовой плазмой, и составляет величину порядка 40-200 км. Поэтому можем сказать, что разрушение озонового слоя (см. ранее) привело к увеличению подъема газовой плазмы в соответствии с фрактальной формой записи (3.35) закона Архимеда (см. п. 3.10), что связано с увеличением поверхностной плотности электрического заряда.
Плазма — это частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При большой температуре резко усиливается процесс термической ионизации. Плазму внутри Земли можно отнести к низкотемпературной, ибо температуру ее можно оценить пример —
но в 1500°С. Свободные заряженные частицы, особенно электроны, легко перемещаются (более правильно — солитоны) под действием электрического поля. Однако на частицы плазмы действуют как магнитное поле Земли, так и ее электрическое поле. Проявление электрической силы на плазму предопределено внутренним строением планеты: внутренняя форма весьма далека от идеальной сферы. Кроме того, на внутренней поверхности оболочки появляются поляризационные заряды, равные по величине и противоположные по знаку зарядам на внешней поверхности. Ведь мы знаем (см. п. 1.2), что полная сила, действующая на тело внутри идеального сферического заряженного тела, равна нулю. Поэтому в реальности любые внешние возмущения вызывают в плазме колебания разного типа [45]. Так как температура и плотность плазмы Земли неоднородны, то также возникают так называемые дрейфовые, ударные, уединенные (солитоны) волны и сильно развитая турбулентность движения. Эти плазменные образования возникают в самом активном слое толщиной около 400 км и оказывают воздействие не только на оболочку планеты, но и своим большим электромагнитным излучением через ее толщину влияют на окружающую атмосферу, среду обитания и на систему жизнеобеспечения, включая работоспособность технических устройств. Все это предопределяет увеличение активности землетрясений, тайфунов, вулканов и т. д. Источником информации об этих процессах являются изменения электрического и магнитного полей Земли. Имея наземную сеть электрометров и магнитометров и учитывая данные геофизической спутниковой системы, мы можем определять надвигающиеся земные процессы с большой точностью.
Заметим, что в центре Земли находится разряженная плазма. Поэтому через ее центр проходят только продольные волны, а поперечные — не проходят, можно сказать, огибают его. Это объясняется тем, что при распространении поперечных волн в плазме с постепенно
меняющейся вдоль оси плотностью происходит искривление их направления движения. Как видите, мы ничего не знали о Земле, ибо нынешняя наука безошибочно может представлять явления и процессы порядка 1%.
Действительно, если вулканы являются естественными регуляторами (клапанами) Земной системы, то разломы, которые появились из-за разрушительной деятельности человека, являются своеобразными коридорами для выхода плазмы. Это подтверждают снимки, сделанные во время исследования дна Тихого океана. По данным американских ученых температура воды этого океана повысилась на 4 —6°С, а среднегодовая температура на Севере — до 3°С. Разрушение дна океанов, озоновые дыры, повышение температуры на Земле обусловливают быстрое таяние ледников Арктики и Антарктиды, что привело к подъему уровня воды в океанах, а это, в свою очередь, вызывает наводнения на всей земной сфере. Глобальное изменение климата обусловливает таяние ледников Северного океана и Антарктиды, что приведет в ближайшие годы к потопу. Выявленные закономерности позволяют предвидеть, что к 2030 году земная цивилизация подойдет к катастрофе. Такая ситуация также прогнозируется в результате анализа данных геофизической спутниковой системы, что видно из последних работ [94, 95].
Заметим, что катастрофическое состояние Земли вызвано незнанием традиционной физикой законов Космоса. Вспомним: глубокое бурение скважин в России (Кольская сверхглубокая скважина глубиной чуть более 12 км) и США (Луизиана, глубина скважины 9600 м) подтвердило, что давление и температура с глубиной возрастают значительно быстрее ожидаемого. Однако не следует заниматься бурением Земли, ибо мы можем создать как отверстие для выхода плазмы, так и вызвать образование искусственного вулкана. Знаем, что наша планета имеет тончайшую оболочку, заполненную газовой плазмой. Оболочка Земли вращается вокруг оси на
экваторе быстрее скорости звука, при этом плазма как бы вращается в обратную сторону вследствие различия плотности их веществ. Поэтому при приближении к экватору толщина оболочки меньше, чем на высоких широтах. Теперь становится понятной картина активной деятельности вулканов: вблизи экватора деятельность вулканов заметно сильнее, чем в самых удаленных от него областях.
Дополним данный раздел информацией о строении Луны. Масса спутника составляет 2,2 • 1019кг, а плотность — 1 кг/м3 (см. табл. 3.2). Масса Луны примерно в 200 раз меньше массы Земли, однако ускорения свободного падения различаются только в 6 раз. По своему строению Луна напоминает строение планеты, однако ее параметры сильно отличаются: толщина оболочки спутника составляет около 2-3 км, внутренность заполнена газом, благодаря которому в основном поддерживается сферическая форма объекта. Прочность Луны обеспечивается как разностью электрических потенциалов видимого и обратного полушариев, так и силой взаимодействия электрических зарядов, расположенных на поверхностях оболочки. Подтверждением такого строения Луны является эксперимент по сбрасыванию груза с орбитальной станции: установленные на поверхности спутника сейсмографы зафиксировали с момента его падения на поверхность долгий гул наподобие звучанию пустой бочки. Поэтому существующий проект сделать Луну вращающимся объектом губителен для человечества. Систему Земля-Луна следует рассматривать как двойную планету [25]. (Двойной планетой следует рассматривать также Плутон, имеющий массивный спутник.) Потеря спутника приведет к повторению ситуации, которая произошла на Венере более 12 тысяч лет назад. Ведь приливные силы (см. далее п. 3.10), создаваемые Луной, также удерживают оболочку планеты от разрушения и не допускают выхода плазмы наружу. Конечно, возможен и второй вариант: Луна превратится в кольцо, опоясывающее
Землю и состоящее из песчинок и камней, наподобие «колец Сатурна».
Так как положительно заряженная Луна делает один оборот за месяц, ее магнитное поле незначительно и составляет около 0,1% от земной напряженности. Электрическое поле Луны отличается от земного не только по •величине (20 В/м), но и по своему направлению, поэтому спутник для жизни человека не пригоден (см. п. 5.2). Однако движение заряженной Луны с запада к востоку (против часовой стрелки) приводит к смещению (запаздыванию) ее выхода над горизонтом в среднем на 50 минут, что оказывает влияние также на нашу жизнь. Такое влияние проявляется в уменьшении биологического суточного ритма человека на 50 минут по сравнению с периодом вращения Земли.
Теперь перейдем к законам построения Солнечной системы. Так как в основе гравитации лежит электрический заряд, то мы можем провести аналогию между величинами и законами, характеризующими схему построения планетной системы и электростатические схемы. Для этого определим электроемкости объектов Солнечной системы. Напомним, коэффициент пропорциональности с между потенциалом и зарядом объекта называется электроемкостью и выражается как q = с • φ. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в то же число раз напряженно -сти Е поля в каждой точке окружающего объект пространства. Соответственно в такое же число раз возрастает работа переноса единичного заряда из бесконечности на поверхность объекта, то есть потенциал объекта.
Исходя из данных таблицы 3.1, произведем вычисление емкостей Солнца, планет и Луны. Так как данные объекты имеют сферическую форму, то потенциал φ = Е.r, где r — радиус объекта. Тогда емкости Солнца — 78 600 мкФ, Меркурия — 269 мкФ, Венеры — 670 мкФ, Земли — 690 мкФ, Марса — 375 мкФ, Юпитера — 7 854
мкФ, Сатурна — б 800 мкФ, Урана — 2 790 мкФ, Нептуна — 2 768 мкФ, Плутона — 128 мкФ, Луны — 194 мкФ. Отсюда можем выразить закон построения Солнечной системы в электрической форме записи (система СИ):
| (3.24) |
cсолнце= Ö4p. åcпланет (3.24)
где åcпланет = 22 344 мкФ. Видим из (3.24), что электроемкость Солнца равна суммарной емкости всех планет, умноженной на Ö4p. Аналогичная связь электро-емкостей Земли и Луны:
Электроемкость уединенного шара зависит от его радиуса и, как показывают расчеты и измерения, численно равна его радиусу. Тогда закон построения Солнечной системы в геометрической форме можем записать как:
rсолнце = Ö4p.årпланет (3.25)
rЗемля=Ö4p.rЛуна
причем rсолнце = 7 • 105 км, årпланет = 2 • 10s км, rЗемля = 6371 км, rЛуна = 1737 км. Связь линейных размеров Солнца и планет, расположенных в одной и той же плоскости, примерно совпадающей с плоскостью солнечного экватора, указывает, что природа сама по себе является вечным двигателем и в то же время униполярным генератором. Благодаря явлению конверсии энергии, которое характеризуется эффективным извлечением энергии из электрической структуры пространства, обеспечивается вечное существование мира в форме движения (см. п. 6.2). Очевидно, что такой закон построения правомерен также для звезд, имеющих планетные системы.
Обратим внимание на величину отношения заряда Солнца к суммарному заряду планет, равную абсолютной величине напряженности электрического поля Солнца (ЕСолице =
6.106В/м):
Этот закон распределения электрического заряда Солнечной системы (3.26) получен из выражения:
В этом выражении
а произведение сомножителей 4p. åcпланет. årпланет / åqпланет = 1.
Действительно, заряд Солнца Q = +3,3.1014 Кл, суммарный заряд планет åqпланет = -5,43.107 Кл, то их отношение равно величине 6.106.
Взаимосвязь электрических зарядов Земли и Луны представляется формулой в виде:
Так как заряд Земли -5,7.105 Кл, заряд Луны +6,8. 103 Кл, то отношение их величин примерно равно 83. Такой порядок величин получаем из соотношения 4p Е3емдя/
ЕЛуна,где Е3емдя = 130 В/м, ЕЛуна = 20 В/м.
Таким образом, установленные законы построения Солнечной системы с большой точностью подтверждаются экспериментальными данными.
Отсюда можно сделать определенный вывод о происхождении Солнечной системы 4,7 млрд. лет тому назад.
Основой создания Солнечной системы явилась комета, падающая к Солнцу под действием его притяжения и по мере своего падения под влиянием электрического поля Солнца она переходила от падения к обращению вокруг Солнца отдельных сформировавшихся сферических образований, которые заняли орбиты примерно в одной плоскости в соответствии с законом сохранения
момента количества движения. Причем планета Плутон являлась ядром кометы, и поэтому она состоит из тяжелых, железно-каменных соединений. Масса планеты Плутон примерно равна массе Земли (см. табл. 3.2 и сравните массы Земли и Плутона с данными [44]: масса Земли 5,98 • 1024, Плутона — 5,4 • 1024 кг), ее плотность составляет 1132,6 кг/м3, что указывает, в отличие от других планет, на однородное пористое строение. Однако нынешняя физика за последние тридцать лет уменьшила массу Плутона в 5 раз [56], а по другим источникам [25] — в 500 раз, чтобы соответственно увязать с реальным ускорением свободного падения и довести среднюю плотность вещества планеты с 1000 000 кг/м3 до 2000 кг/м3 [102].
Обратим внимание, что средняя плотность вещества планет не может превышать 1158 кг/м3 — плотности Солнца, ибо в противном случае процесс создания сферических образований не был возможен. Для понимания укажем, что сила нормальной реакции Солнца, действовавшая в процессе создания Солнечной системы на сформировавшуюся планету, пропорциональна разности плотностей звезды и образования. Закономерно, что такая соразмерность средней плотности вещества планет со средней плотностью центра тяготения правомерна для всех планетных образований во Вселенной.
Подтверждением такого происхождения Солнечной системы являются астероиды и кометы, которые представляют собой остатки вещества, являвшегося «кирпичиками» при образовании планет. Кроме того, на это указывают локальные фрактальные размерности, выражающие отношения масс планет и Луны к их заряду. Они различны для каждого образования. Для Земли отношение массы к ее заряду составляет 0,8.1016, для Луны — 0,3 • 1016, для Венеры — 0,5 • 1016 (по величине совпадает с размерностью Солнца и Галактики), для Меркурия — 0,2 . 1016, для Марса — 1,6 • 1016, для Юпитера — 0,1 • 1018, для Сатурна — 0,3 • 1018, для Урана — 0,8 •
l618, для Нептуна — 1 .1018, для Плутона — 2,2 .1018. При этом заметим, фрактальные размерности Земли и Луны в принципе имеют противоположные знаки, поэтому их сумма равна размерности Венеры и по величине совпадает с размерностью Солнца и Галактики (см. п. 3.7). Такая фрактальная соразмерность Земли и Венеры указывает на возможное повторение на нашей планете венерского сценария при потере спутника.
Также установлена связь фрактальной размерности Солнечной системы с локальной фрактальной размерностью планеты Плутон:
(3.27)
причем å(m/q)планет = 4,4 . 1018. Очевидно, данное действие фрактальной геометрии подобно определению диаметра Солнечной системы по радиусу орбиты планеты Плутон в случае евклидовой геометрии. Далее просматривается связь локальной фрактальной размерности планеты Плутон с соответствующей размерностью Солнца:
(3.28)
причем в (3.28) сомножитель Е2Плутон для согласования размерностей следует учитывать только его величину. Знаем, что напряженность EПлутон = 21 В/м, Для вывода данной формулы следует заметить, что фрактальные размерности Солнца и Венеры по величине совпадают (см. ранее). Поэтому Венера имеет из всех планет самую большую энергию в спектре отраженного солнечного излучения.
Заметим, однако, что гравитационное взаимодействие в Солнечной системе характеризуется не только силами притяжения, но и отталкивания, приводящими к возмущениям орбит планет Солнечной системы. Так, возмущения, наблюдаемые в движении Нептуна [24], можно объяснить воздействием других планет, тоже заряженных отрицательно. Уже началось электрическое влияние
надвигающегося 5 мая 2000 г. малого парада планет [94, 95] на ротационное движение Земли. Однако до настоящего времени при исследовании Солнечной системы никогда не производилось измерений электрических полей планет и их спутников, за исключением Земли. Это говорит о несостоятельности нынешней физики.
Таким образом, новая физика отвергла неверный закон тяготения инертных масс, установила природу гравитации (тяготения), реальные параметры планет, законы построения Солнечной системы и ее происхождение.
В чем физический смысл этого числа?
Если в формулу, которая дана для закона всемирного тяготения, подставить конкретные числа, то получится интересный результат. В частном случае, когда массы тел равны 1 килограмму, а расположены они на расстоянии 1 метра, сила тяготения оказывается равной самому числу, которое известно для гравитационной постоянной.
То есть смысл гравитационной постоянной заключается в том, что она показывает, с какой силой будут притягиваться такие тела на расстоянии одного метра. По числу видно, насколько мала эта сила. Ведь она в десять миллиардов меньше единицы. Ее даже невозможно заметить. Даже при увеличении тел в сотню раз результат существенно не изменится. Он по-прежнему останется гораздо меньше единицы. Поэтому становится понятно, отчего сила притяжения заметна только в тех ситуациях, если хотя бы одно тело имеет огромную массу. Например, планета или звезда.

Физики уточнили значение гравитационной постоянной в четыре раза


Qing Li et al. / Nature
Физики из Китая и России уменьшили погрешность гравитационной постоянной в четыре раза — до 11,6 частей на миллион, поставив две серии принципиально разных опытов и уменьшив до минимума систематические погрешности, искажающие результаты. Статья опубликована в Nature
.
Впервые гравитационную постоянную G
, входящую в закон всемирного тяготения Ньютона, измерил в 1798 году британский физик-экспериментатор Генри Кавендиш. Для этого ученый использовал крутильные весы, построенные священником Джоном Мичеллом. Простейшие крутильные весы, конструкция которых была придумана в 1777 году Шарлем Кулоном, состоят из вертикальной нити, на которой подвешено легкое коромысло с двумя грузами на концах. Если поднести к грузам два массивных тела, под действием силы притяжения коромысло начнет поворачиваться; измеряя угол поворота и связывая его с массой тел, упругими свойствами нити и размерами установки, можно вычислить значение гравитационной постоянной. Более подробно с механикой крутильных весов можно разобраться, решая соответствующую задачу.
Полученное Кавендишем значение для постоянной составило G
= 6,754×10−11 ньютонов на метр квадратный на килограмм, а относительная погрешность опыта не превышала одного процента.


Модель крутильных весов, с помощью которых Генри Кавендиш впервые измерил гравитационное притяжение между лабораторными телами
Science Museum / Science & Society Picture Library
Поделиться
С тех пор ученые поставили более двухсот экспериментов по измерению гравитационной постоянной, однако так и не смогли существенно улучшить их точность. В настоящее время значение постоянной, принятое Комитетом данных для науки и техники (CODATA) и рассчитанное по результатам 14 наиболее точных экспериментов последних 40 лет, составляет
G
= 6,67408(31)×10−11 ньютонов на метр квадратный на килограмм (в скобках указана погрешность последних цифр мантиссы). Другими словами, ее относительная погрешность примерно равна 47 частей на миллион, что всего в сто раз меньше, чем погрешность опыта Кавендиша и на много порядков больше, чем погрешность остальных фундаментальных констант. Например, ошибка измерения постоянной Планка не превышает 13 частей на миллиард, постоянной Больцмана и элементарного заряда — 6 частей на миллиард, скорости света — 4 частей на миллиард. В то же время, физикам очень важно знать точное значение постоянной
G
, поскольку оно играет ключевую роль в космологии, астрофизике, геофизике и даже в физике частиц. Кроме того, высокая погрешность постоянной мешает переопределить значения других физических величин.
Скорее всего, низкая точность постоянной G
связана со слабостью сил гравитационного притяжения, которые возникают в наземных экспериментах, — это мешает точно измерить силы и приводит к большим систематическим погрешностям, обусловленным конструкцией установок. В частности, заявленная погрешность некоторых экспериментов, использованных при расчете значения CODATA, не превышала 14 частей на миллион, однако различие между их результатами достигало 550 частей на миллион. В настоящее время не существует теории, которая могла бы объяснить такой большой разброс результатов. Скорее всего, дело в том, что в некоторых экспериментах ученые упускали из виду какие-то факторы, которые искажали значения постоянной. Поэтому все, что остается физикам-экспериментаторам — уменьшать систематические погрешности, минимизируя внешние воздействия, и повторять измерения на установках с принципиально разной конструкцией.
Именно такую работу провела группа ученых под руководством Цзюнь Ло (Jun luo) из Университета науки и технологий Центрального Китая при участии Вадима Милюкова из ГАИШ МГУ.
Для уменьшения погрешности исследователи повторяли опыты на нескольких установках с принципиально разной конструкцией и различными значениями параметров. На установках первого типа постоянная измерялась с помощью метода TOS (time-of-swing), в котором величина G
определяется по частоте колебаний крутильных весов. Чтобы повысить точность, частота измеряется для двух различных конфигураций: в «ближней» конфигурации внешние массы находятся поблизости от равновесного положения весов (эта конфигурация представлена на рисунке), а в «дальней» — перпендикулярно равновесному положению. В результате частоты колебаний в «дальней» конфигурации оказывается немного меньше, чем в «ближней» конфигурации, и это позволяет уточнить значение
G
.
С другой стороны, установки второго типа полагались на метод AAF (angular-acceleration-feedback) — в этом методе коромысло крутильных весов и внешние массы вращаются независимо, а их угловое ускорение измеряется с помощью системы управления с обратной связью, которая поддерживает нить незакрученной. Это позволяет избавиться от систематических ошибок, связанных с неоднородностью нити и неопределенностью ее упругих свойств.
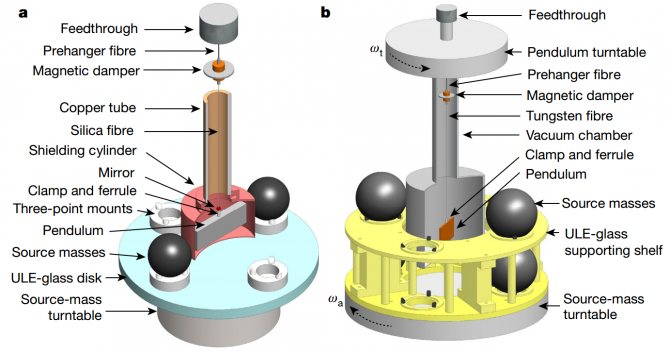

Схема экспериментальных установок по измерению гравитационной постоянной: метод TOS (a) и AAF (b)
Qing Li et al. / Nature
Поделиться


Фотографии экспериментальных установок по измерению гравитационной постоянной: метод TOS (a–c) и AAF (d–f)
Qing Li et al. / Nature
Поделиться
Кроме того, физики постарались до минимума сократить возможные систематические ошибки. Во-первых, они проверили, что гравитирующие тела, участвующие в опытах, действительно однородны и близки к сферической форме — построили пространственное распределение плотности тел с помощью сканирующего электронного микроскопа, а также измерили расстояние между геометрическим центром и центром масс двумя независимыми методами. В результате ученые убедились, что колебания плотности не превышают 0,5 части на миллион, а эксцентриситет — одной части на миллион. Кроме того, исследователи поворачивали сферы на случайный угол перед каждым из опытов, чтобы скомпенсировать их неидеальности.
Во-вторых, физики учли, что магнитный демпфер, который используется для подавлений нулевых мод колебаний нити, может вносить вклад в измерение постоянной G
, а затем изменили его конструкцию таким образом, чтобы этот вклад не превышал нескольких частей на миллион.
В-третьих, ученые покрыли поверхность масс тонким слоем золотой фольги, чтобы избавиться от электростатических эффектов, и пересчитали момент инерции крутильных весов с учетом фольги. Отслеживая электростатические потенциалы частей установки в ходе опыта, физики подтвердили, что электрические заряды не влияют на результаты измерений.
В-четвертых, исследователи учли, что в методе AAF кручение происходит в воздухе, и скорректировали движение коромысла с учетом сопротивления воздуха. В методе TOS все части установки находились в вакуумной камере, поэтому подобные эффекты можно было не учитывать.
В-пятых, экспериментаторы поддерживали температуру установки постоянной в течение опыта (колебания не превышали 0,1 градуса Цельсия), а также непрерывно измеряли температуру нити и корректировали данные с учетом едва заметных изменений ее упругих свойств.
Наконец, ученые учли, что металлическое покрытие сфер позволяет им взаимодействовать с магнитным полем Земли, и оценили величину этого эффекта. В ходе эксперимента ученые каждую секунду считывали все данные, включая угол поворота нити, температуру, колебания плотности воздуха и сейсмические возмущения, а затем строили полную картину и рассчитывали на ее основании значение постоянной G
.
Каждый из опытов ученые повторяли много раз и усредняли результаты, а затем изменяли параметры установки и начинали цикл сначала. В частности, опыты с использованием метода TOS исследователи провели для четырех кварцевых нитей различного диаметра, а в трех экспериментах со схемой AAF ученые изменяли частоту модулирующего сигнала. На проверку каждого из значений физикам понадобилось около года, а суммарно эксперимент продлился более трех лет.
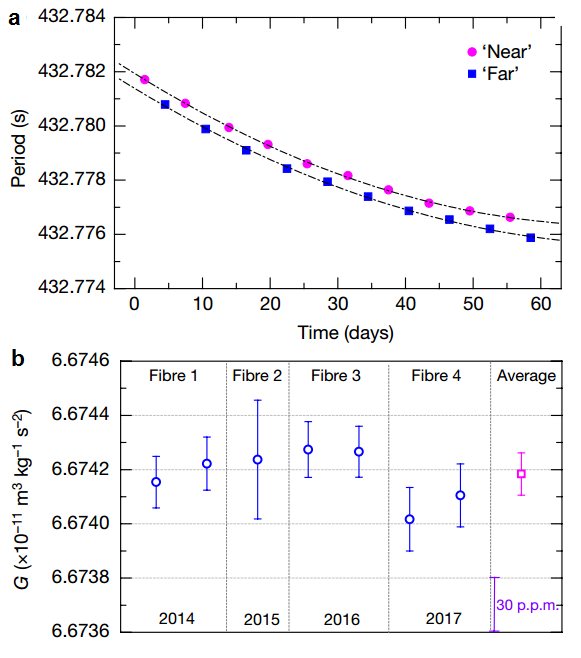

(a) Зависимость от времени периода колебаний крутильных весов в методе TOS; сиреневые точки отвечают «ближней» конфигурации, синие — «дальней». (b) Усредненные значения гравитационной постоянной для различных установок TOS
Qing Li et al. / Nature
Поделиться


(a) Зависимость от времени углового ускорения крутильных весов в методе AAF. (b) Усредненные значения гравитационной постоянной для различных установок AAF
Qing Li et al. / Nature
Поделиться
В результате ученые получили усредненные значения гравитационной постоянной
G
= 6,674184(78)×10−11 ньютон на метр квадратный на килограмм для метода TOS и
G
= 6,674484(78)×10−11 ньютон на метр квадратный на килограмм для метода AAF. Относительные погрешности в каждом случае примерно равны 11,6 частей на миллион. На данный момент это самые точные значения гравитационной постоянной. Кроме того, авторы отмечают, что эти значения получены с помощью усреднения данных различных установок, а потому должны быть избавлены от систематических погрешностей. Правда, авторы статьи так и не смогли объяснить расхождение между значениями постоянной, полученных методом TOS и AAF, которое составляет почти 45 частей на миллион.
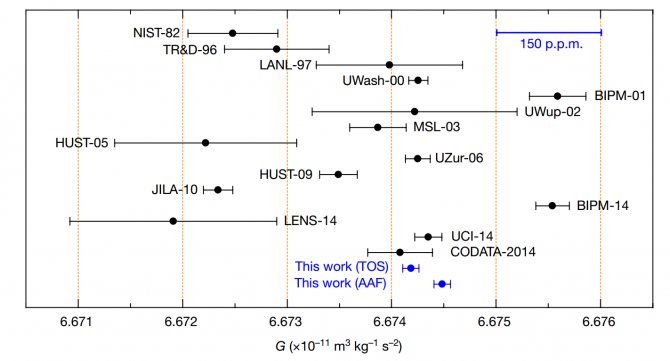

Значения гравитационной постоянной, определенные в различных экспериментах. Новые результаты отмечены синим цветом
Qing Li et al. / Nature
Поделиться
Возможно, в будущем ученые смогут еще сильнее уточнить значение гравитационной постоянной с помощью космических экспериментов: в мае 2020 года группа астрономов из США и Германии предложила план первого эксперимента, который обещает уменьшить погрешность постоянной почти в тысячу раз. К сожалению, до экспериментальной реализации этой идеи пока еще далеко.
В настоящее время ученые стараются выразить все физические величины через фундаментальные константы, чтобы добиться большей универсальности экспериментов и повысить точность их результатов. В частности, с этой целью в 1983 году было принято определение метра через скорость света, а в последнее время предпринимаются попытки переопределить температуру и массу. Подробнее прочитать про назревающие изменения системы СИ можно в нашем материале «Последний эталон».
Дмитрий Трунин
Как связана гравитационная постоянная с ускорением свободного падения?
Если сравнить две формулы, одна из которых будет для силы тяжести, а другая для закона тяготения Земли, то можно увидеть простую закономерность. Гравитационная постоянная, масса Земли и квадрат расстояния от центра планеты составляют коэффициент, который равен ускорению свободного падения. Если записать это формулой, то получится следующее:
- g = (G х M) : r2.
Причем в ней используются такие обозначения:
| Масса Земли | M |
| Радиус Земли | r |
Кстати, гравитационную постоянную можно найти и из этой формулы:
- G = (g х r2) : M.
Если требуется узнать ускорение свободного падения на некоторой высоте над поверхностью планеты, то пригодится такая формула:
- g = (G х M) : (r + н)2, где н — высота над поверхностью Земли.
История измерения[ | ]
Основная статья: Эксперимент Кавендиша
Гравитационная постоянная фигурирует в современной записи закона всемирного тяготения, однако отсутствовала в явном виде у Ньютона и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная в нынешнем виде впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном в «Трактате по механике» (1809), по крайней мере никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявлено[источник не указан 1046 дней
].
В 1798 году Генри Кавендиш поставил эксперимент с целью определения средней плотности Земли с помощью крутильных весов, изобретённых Джоном Мичеллом (Philosophical Transactions 1798). Кавендиш сравнивал маятниковые колебания пробного тела под действием тяготения шаров известной массы и под действием тяготения Земли. Численное значение гравитационной постоянной было вычислено позже на основе значения средней плотности Земли. Точность измеренного значения G
со времён Кавендиша увеличилась, но и его результат[5] был уже достаточно близок к современному.
Значение этой постоянной известно гораздо менее точно, чем у всех других фундаментальных физических постоянных, и результаты экспериментов по её уточнению продолжают различаться[6][7].
В то же время известно, что проблемы не связаны с изменением самой постоянной от места к месту и во времени (неизменность
гравитационной постоянной проверена с точностью до Δ
G
/
G
~ 10−17), но вызваны экспериментальными трудностями измерения малых сил с учётом большого числа внешних факторов[8]. В будущем, если опытным путём будет установлено более точное значение гравитационной постоянной, то оно может быть пересмотрено[9][10].
В 2013 г. значение гравитационной постоянной было получено группой ученых, работавших под эгидой Международного бюро мер и весов:
G
= 6,67554(16) × 10−11 м3·с−2·кг−1 (стандартная относительная погрешность 25 ppm (или 0,0025 %), первоначальное опубликованное значение несколько отличалось от окончательного из-за ошибки в расчётах и было позже исправлено авторами)[11][12].
В июне 2014 года в журнале «Nature» появилась статья итальянских и нидерландских физиков, где были представлены новые результаты измерения G
, сделанные при помощи атомных интерферометров[13]. По их результатам
G
= 6,67191(99) × 10−11 м3·с−2·кг−1 с погрешностью 0,015 % (150 ppm).
Авторы указывают, что поскольку эксперимент с применением атомных интерферометров основан на принципиально других подходах, он помогает выявить некоторые систематические ошибки, не учитывающиеся в других экспериментах.
В августе 2020 года в журнале «Nature» физиками из Китая и России были опубликованы[14] результаты новых измерений гравитационной постоянной с улучшенной точностью (погрешность 12 ppm, или 0,0012 %). Были использованы два независимых метода — измерение времени качаний торсионного подвеса и измерение углового ускорения, получены значения G
, соответственно:
G
= 6,674184(78) × 10−11 м3·с−2·кг−1;
G
= 6,674484(78) × 10−11 м3·с−2·кг−1.
Оба результата в пределах двух стандартных отклонений совпадают с рекомендованным значением CODATA, хотя отличаются друг от друга на ~2,5 стандартных отклонения.
По астрономическим данным постоянная G
практически не изменялась за последние сотни миллионов лет, скорость её относительного изменения (d
G
/d
t
)/
G
не превышает нескольких единиц на 10−11 в год[15][16][17].