Смещение перигелия Меркурия Википедия

Схема смещения орбиты Меркурия, вид с северного полюса эклиптики
Аномальное смещение перигелия Меркурия

— обнаруженная в 1859 году особенность движения планеты Меркурий, сыгравшая исключительную роль в истории физики[1]. Это смещение оказалось первым движением небесного тела, которое не подчинялось ньютоновскому закону всемирного тяготения[комм. 1][1]. Физики были поставлены перед необходимостью искать пути модифицировать или обобщить теорию тяготения. Поиски увенчались успехом в 1915 году, когда Альберт Эйнштейн разработал общую теорию относительности (ОТО); из уравнений ОТО вытекало именно такое значение смещения, которое фактически наблюдалось. Позже были измерены аналогичные смещения орбит нескольких других небесных тел, значения которых также совпали с предсказанными ОТО.

Лауреат Нобелевской премии по физике Ричард Фейнман заметил[2], что долгое время ньютоновская теория тяготения полностью подтверждалась наблюдениями, но для объяснения едва заметного отклонения в движении Меркурия потребовалась коренная перестройка всей теории на основе нового понимания гравитации.

Содержание

1 Открытие эффекта
2 Попытки объяснения в рамках классической теории тяготения 2.1 Вулкан и вулканоиды
2.2 Другие гипотетические объекты внутри орбиты Меркурия
2.3 Заниженная масса планет
2.4 Другие попытки объяснения
2.5 Критика со стороны Саймона Ньюкома

3 Предложения по модификации классической теории тяготения

3.1 Модели без зависимости от скорости

3.2 Модели с зависимостью от скорости

4 Решение в рамках общей теории относительности

5 Механизм гравитационного взаимодействия с точки зрения квантовой теории гравитации

6 См. также

7 Примечания

8 Литература

9 Ссылки

Открытие эффекта[править | править код]

Параметры орбит планет Солнечной системы из-за взаимовлияния этих планет со временем претерпевают медленные изменения. В частности, ось орбиты Меркурия постепенно поворачивается (в плоскости орбиты) в сторону орбитального движения[3], соответственно, смещается и ближайшая к Солнцу точка орбиты — перигелий («прецессия перигелия»). Угловая скорость поворота составляет примерно 500″ (угловых секунд) за 100 земных лет, так что в исходное положение перигелий возвращается каждые 260 тыс. лет[4].

Урбен Леверье

В середине XIX века астрономические расчёты движения небесных тел, основанные на ньютоновской теории тяготения, давали чрезвычайно точные результаты, неизменно подтверждаемые наблюдениями («астрономическая точность» вошла в поговорку). Триумфом небесной механики в 1846 году стало открытие Нептуна в теоретически предсказанном месте небосвода.

В 1840—1850-е годы французский астроном Урбен Леверье, один из первооткрывателей Нептуна, на основе 40-летних наблюдений Парижской обсерватории разработал теорию движения Меркурия. В своих статьях 1859 года[5][6] Леверье сообщил, что в 1846 году обнаружил небольшое, но существенное расхождение теории с наблюдениями — перигелий смещался несколько быстрее, чем следовало из теории. В своих расчётах Леверье учёл влияние всех планет[4]:

Планета	Вклад в смещение перигелия Меркурия (в угловых секундах за столетие)
Венера	280,6
Земля	083,6
Марс	002,6
Юпитер	152,6
Сатурн	007,2
Уран	000,1

В итоге рассчитанное Леверье теоретическое значение смещения составило 526,7″ за столетие, а наблюдения показали примерно 565″. По современным уточнённым данным, смещение несколько выше и равно 570″. Таким образом, разница составляет около 43″ за столетие. Хотя это различие невелико, оно значительно превышает погрешности наблюдения и нуждается в объяснении[7].

Для решения проблемы аномалии выдвигались гипотезы в основном двух типов.

«Материальные гипотезы»: смещение вызвано влиянием какой-то материи вблизи Солнца.
Новые теории тяготения, отличные от ньютоновской.

Открытие эффекта

Урбен Леверье

Планета	Вклад в смещение перигелия Меркурия (в угловых секундах за столетие)
Венера	280,6
Земля	083,6
Марс	002,6
Юпитер	152,6
Сатурн	007,2
Уран	000,1

В итоге рассчитанное Леверье теоретическое значение смещения составило 526,7″ за столетие, а наблюдения показали примерно 565″. По современным уточнённым данным смещение несколько выше и равно 570″. Таким образом, разница составляет около 43″ за столетие. Хотя это различие невелико, оно значительно превышает погрешности наблюдения и нуждается в объяснении[7].

Для решения проблемы аномалии выдвигались гипотезы в основном двух типов.

«Материальные гипотезы»: смещение вызвано влиянием какой-то материи вблизи Солнца.
Новые теории тяготения, отличные от ньютоновской.

Попытки объяснения в рамках классической теории тяготения[править | править код]

Вулкан и вулканоиды[править | править код]

Леверье предположил, что аномалия объясняется наличием неизвестной планеты (или нескольких малых планет) внутри орбиты Меркурия. Эту гипотезу поддержал авторитетный французский астроном Франсуа Феликс Тиссеран. По предложению физика Жака Бабинэ гипотетической планете дали имя «Вулкан». Из-за её близости к Солнцу наилучшим способом обнаружить Вулкан были наблюдения во время солнечного затмения или во время прохождения Вулкана между Землёй и Солнцем; в последнем случае планета была бы видна как тёмное пятно, быстро пересекающее солнечный диск[8].

Предполагаемая орбита Вулкана (VULCAN) на схеме внутренних планет Солнечной системы

Вскоре после публикаций 1859 года французский астроном-любитель Эдмон Лескарбо (Edmond Modeste Lescarbault

) сообщил Леверье, что в 1845 году наблюдал перед Солнцем тёмный объект, зарегистрировал его координаты, однако тогда не придал наблюдению должного значения. Леверье по результатам Лескарбо вычислил, что объект втрое ближе к Солнцу, чем Меркурий, период обращения составляет 19 дней 7 часов, диаметр около 2000 км. При этом, если плотность Вулкана близка к плотности Меркурия, его масса составляет 1/17 массы Меркурия. Однако тело с такой небольшой массой не может вызвать наблюдаемый сдвиг перигелия Меркурия, поэтому Леверье предположил, что Вулкан — не единственная малая планета между Меркурием и Солнцем. Он рассчитал примерную орбиту Вулкана и в 1860 году, когда ожидалось полное солнечное затмение, призвал астрономов всего мира посодействовать в обнаружении Вулкана. Все наблюдения оказались безрезультатны[9].

Планету искали несколько десятилетий, но по-прежнему безо всякого успеха. Были ещё несколько неподтвердившихся сообщений об открытии — за новую планету принимали солнечные протуберанцы, солнечные пятна, а также звёзды и мелкие околоземные астероиды, близко расположенные к диску Солнца во время затмения. После каждого такого сообщения астрономы заново рассчитывали орбиту предполагаемого Вулкана и ждали, что при следующем прохождении перед Солнцем планета будет повторно найдена, но она больше не появлялась[8]. Последние сообщения о возможном открытии Вулкана были опубликованы в начале 1970-х годов, причиной оказалось падение кометы на Солнце[9].

Вариант с несколькими малыми планетами, которых заранее назвали «Вулканоидами», был также тщательно проверен. Леверье верил в существование Вулкана или вулканоидов до конца жизни (1877), однако ни одного прохождения сколько-нибудь крупного неизвестного объекта по диску Солнца достоверно зарегистрировать не удалось[10]. В 1909 году американский астроном Уильям Уоллес Кэмпбелл уже имел основания уверенно заявить, что между Меркурием и Солнцем нет объектов крупнее 50 км в диаметре[8].

Другие гипотетические объекты внутри орбиты Меркурия[править | править код]

Гуго Ганс фон Зелигер
Как альтернатива высказывалось предположение о существовании неизвестного спутника Меркурия (возможно, нескольких спутников). Их поиск также не имел успеха[11]. Ещё одна гипотеза, которую высказал в 1906 году немецкий астроном Гуго Ганс фон Зелигер, допускала наличие вокруг Солнца рассеянного (диффузного) облака вещества, видимым признаком которого служит зодиакальный свет. Это облако, по Зелигеру, наклонено к плоскости эклиптики и слабо влияет на движение планет. Скептики возражали, что для смещения перигелия Меркурия это облако должно обладать значительной массой, но тогда от него следует ожидать гораздо более высокий уровень светимости; кроме того, массивное облако неизбежно влияло бы на движение Венеры, в котором серьёзных необъяснимых аномалий не отмечается[12][13].

Голландский метеоролог Христофор Бёйс-Баллот в 1849 году, ещё до работ Леверье, предположил, что Солнце, подобно Сатурну, окружено кольцом (возможно, даже двумя кольцами). Леверье и другие учёные отвергли эту гипотезу, указав, что такие кольца не смогут стабильно существовать вблизи Солнца, да и сама гипотеза плохо аргументирована[14].

Заниженная масса планет[править | править код]

Причиной аномалии могла стать заниженная оценка массы одной из планет (под наибольшее подозрение подпадала Венера). Однако против этого предположения свидетельствовал тот факт, что, будь оно верно, аномалии из-за неверной массы обнаружились бы и в рассчитанных движениях других планет. Французский астроном Эммануэль Ляи предположил, что эффект вызван наложением нескольких причин: рефракции, немного заниженной массы Венеры и ошибок наблюдения; после исследований Ньюкома (см. ниже) реальное существование аномалии больше не подвергалось сомнению[15].

Другие попытки объяснения[править | править код]

Среди возможных причин смещения перигелия Меркурия называлось осевое сжатие Солнца у полюсов. Наблюдения, однако, не обнаружили у Солнца сжатия, достаточного для объяснения эффекта[16]. По данным измерений 1975 года, осевое сжатие солнечного диска составляет всего 0,018 4 ± 0,012 5 {\displaystyle 0{,}0184\pm 0{,}0125} угловых секунд[17].

С 1870-х годов начали появляться первые гипотезы о том, что источник аномалии связан с неевклидовой геометрией Вселенной (Шеринг, Киллинг, позднее (1900-е годы) Шварцшильд и Пуанкаре)[18]. Немецкий астроном Пауль Харцер[de] склонялся к мнению, что кривизна пространства положительна, поскольку тогда объём Вселенной конечен, и такие проблемы, как гравитационный и фотометрический парадоксы, отпадают[19]. Однако объяснить смещение перигелия Меркурия с помощью этой гипотезы не удалось — расчёты показали, что для этого требуется неправдоподобно большая кривизна пространства[18].

Гуго Ганс фон Зелигер в 1906 году исследовал гипотезу своего ученика, астронома Эрнста Андинга (Ernst Anding

): система координат, связанная с неподвижными звёздами, неинерциальна, а связанная с планетами — инерциальна. Это необычное предположение позволяло с помощью подбора параметров объяснить все известные планетные аномалии. Андинг также постулировал существование нескольких пылевых облаков, создающих зодиакальный свет вблизи Солнца. Многие учёные подвергли модель Андинга — Зелигера уничтожающей критике как искусственную и с точки зрения физики неправдоподобную — в частности, Эрвин Фройндлих и Гарольд Джеффрис доказали, что источник зодиакального света слишком разрежён, чтобы иметь требуемую в модели массу[20].

Критика со стороны Саймона Ньюкома[править | править код]

Саймон Ньюком
В 1895 году свои результаты расчётов орбит четырёх внутренних планет (Меркурия, Венеры, Земли и Марса) опубликовал ведущий американский астроном Саймон Ньюком. Он подтвердил наличие аномалии в движении Меркурия и уточнил её значение: 43″ вместо 38″ у Леверье[21]. В существование неизвестных планет внутри орбиты Меркурия Ньюком не верил и заявил, что эта гипотеза «совершенно исключается», а массу Венеры он сам уточнил, похоронив все предположения, что её оценка существенно занижена[22].

Ньюком обнаружил смещение перигелия не только у Меркурия, но и у Марса, а также, с меньшей уверенностью, у Венеры и Земли (их орбиты почти круговые, поэтому отмеченное для этих двух планет смещение было близко к погрешности измерения)[22]. При этом была окончательно отвергнута гипотеза Бёйс-Баллота о кольце вокруг Солнца, потому что никаким подбором его параметров не удаётся получить реальное смещение и для Меркурия, и для Марса одновременно; аналогичные трудности вызывало предположение о системе астероидов. Ньюком указал также, что как гипотетическое кольцо, так и массивная диффузная материя вблизи Солнца вызвали бы смещение узлов орбиты Венеры и самого Меркурия, не согласующееся с наблюдениями[23]. Наблюдения и расчёты Ньюкома подтвердил авторитетный французский астроном Франсуа Феликс Тиссеран[18].

Меркурий подрался и сошел с орбиты

Автор Антон Евсеев

Обновлено: 19.12.2011 11:59 Опубликовано: 16.12.2011 07:00

Наука » Экология » Космос

Группа астрофизиков из Парижского университета имени Дидро предложило гипотезу, которая объясняет, почему Меркурий вращается вокруг Солнца совсем не так, как ему бы следовало это делать. С их точки зрения, в этом виновата «детская травма» — столкновение этой небольшой планеты с крупными астероидами на заре формирования Солнечной системы.

3 поделились

Самая маленькая планета Солнечной системы Меркурий (а таковой он стал тогда, когда в 2006 году Плутон лишили гордого звания планеты) еще к тому же самая… неправильная. Конечно же, этого следовало ожидать от небесного тела с подобным названием, поскольку, как мы помним, вестник богов Меркурий всегда отличался странным, а временами даже просто асоциальным поведением. Однако некоторые «выверты» данной планеты просто поражают воображение ученых. И далеко не все они могут быть объяснены с точки зрения астрофизики.

Например, расчеты и данные наблюдений достаточно долгое время говорили о том, что день на Меркурии должен быть равен году. Напомню, что эта самая близкая к Солнцу планета совершает свой оборот вокруг светила за 87,97 земных суток. И оборот вокруг своей оси он совершает, как считали астрофизики, примерно за столько же. Именно поэтому многие думали, что Меркурий постоянно обращен к Солнцу одной и той же стороной.

Предложения по модификации классической теории тяготения[править | править код]

Попытки улучшить ньютоновский закон всемирного тяготения предпринимались начиная с середины XVIII века. Первую попытку сделал в 1745 году А. К. Клеро, чтобы объяснить аномалии в движении Луны. В мемуаре «О системе мира согласно началу тяготения

» Клеро предложил вместо ньютоновского закона:
F = G ⋅ m 1 ⋅ m 2 R 2 {\displaystyle F=G\cdot {m_{1}\cdot m_{2} \over R^{2}}}
другую, более общую формулу:

F = G ⋅ m 1 ⋅ m 2 ( 1 R 2 + a R 4 ) {\displaystyle F=G\cdot {m_{1}\cdot m_{2}\left({\frac {1}{R^{2}}}+{\frac {a}{R^{4}}}\right)}}

Здесь F {\displaystyle F} — сила тяготения, m 1 , m 2 {\displaystyle m_{1},m_{2}} — массы тел, R {\displaystyle R} — расстояние между телами, G {\displaystyle G} — гравитационная постоянная, равная 6,673 84 ( 80 ) ⋅ 10 − 11 {\displaystyle 6{,}67384(80)\cdot 10^{-11}} м³/(кг с²), a {\displaystyle a} — дополнительная калибровочная константа.

Позже (1752 год) Клеро пришёл к выводу, что для объяснения движения Луны, со всеми замеченными аномалиями, вполне достаточно классического закона. Окончательные результаты своих трудов Клеро свёл в трактат, названный «Теория Луны, выведенная из единственного начала притяжения, обратно пропорционального квадратам расстояний

». Тем не менее идея Клеро, в различном математическом оформлении, неоднократно возникала в истории астрономии, в том числе для объяснения смещения перигелия Меркурия[24].

Модели без зависимости от скорости[править | править код]

В статье 1895 года Саймон Ньюком исследовал способ объяснения аномалии, связанный с модификацией закона всемирного тяготения. Простейшая модификация состоит в замене квадрата расстояния на немного бо́льшую степень:

F = G ⋅ m 1 ⋅ m 2 R 2 + δ {\displaystyle F=G\cdot {m_{1}\cdot m_{2} \over R^{2+\delta }}}

Тогда смещение перигелия за один оборот будет равно[25]:

2 π 1 − δ ≈ 2 π ( 1 + δ 2 ) , {\displaystyle {\frac {2\pi }{\sqrt {1-\delta }}}\approx 2\pi \left(1+{\frac {\delta }{2}}\right),}

то есть дополнительное смещение равно δ π . {\displaystyle \delta \pi .}

Это предположение известно как «гипотеза Холла», американский астроном Асаф Холл опубликовал её годом раньше (1894)[26]. Значение δ = 0,000 000 157 4 {\displaystyle \delta =0{,}000\,000\,157\,4} позволяет объяснить аномальное смещение перигелия Меркурия[27]. Дополнительным достоинством нового закона тяготения по сравнению с ньютоновским был тот факт, что он не создавал гравитационный парадокс[28] — потенциал поля тяготения бесконечной Вселенной не обращался в бесконечность.

Ряд учёных (в частности, Вебер и Ритц) проявили интерес к такому подходу, хотя были и критики — указывали, например, на то, что в законе Холла постоянной тяготения G {\displaystyle G} приходится приписывать дробную размерность длины. К тому же расчёты Ньюкома показали, что смещение перигелия Марса по новому закону получается далёким от фактического[29].

Исследовался и несколько более общий вариант закона тяготения — добавление в формуле Ньютона выражения, обратно пропорционального R 3 {\displaystyle R^{3}} или R 4 {\displaystyle R^{4}} . Однако Ньюком отверг и этот вариант, поскольку из него следовало, например, что притяжение двух близких предметов на Земле неправдоподобно велико[30][31].

Зелигер и Нейман предложили ещё одну модификацию закона всемирного тяготения:

F = G ⋅ m 1 ⋅ m 2 R 2 e − λ R {\displaystyle F=G\cdot {m_{1}\cdot m_{2} \over R^{2}}e^{-\lambda R}}

В ней дополнительный множитель e − λ R {\displaystyle e^{-\lambda R}} обеспечивает более быстрое, чем у Ньютона, убывание тяготения с расстоянием. Подбор коэффициента затухания λ {\displaystyle \lambda } позволял также объяснить смещение перигелия Меркурия, однако и в этом случае движение Венеры, Земли и Марса переставало соответствовать наблюдениям[32].

В 1897 году американский астроном Эрнест Уильям Браун опубликовал очень точные таблицы движения Луны, значительно подорвавшие доверие к гипотезе Холла[33]. Одновременно (1896) Гуго Ганс фон Зелигер исследовал три варианта модификации закона Ньютона, включая закон Холла, и показал, что все они не согласуются с наблюдениями. В 1909 году Ньюком также пришёл к выводу, что гравитационное поле описывается классическим законом Ньютона[34].

Модели с зависимостью от скорости[править | править код]

Некоторые физики предлагали ввести в закон тяготения зависимость силы от скорости тел[31]. Меркурий отличается от других планет не только близостью к Солнцу, но и большей скоростью, поэтому возникли предположения, что именно скорость ответственна за дополнительное смещение перигелия. Авторы этих идей ссылались также на законы электродинамики, где зависимость силы от скорости была общепринятой[35].

Первые модели подобного рода, разработанные во второй половине XIX века по аналогии с электродинамикой Вебера или Максвелла, давали слишком маленькое значение смещения перигелия (не более 6—7″ в столетие). Их авторы вынуждены были предположить, что, возможно, часть аномалии имеет причиной зависимость тяготения от скорости, а остальная часть — влияние какого-то неизвестного вещества вблизи Солнца[35]. Несмотря на то, что этой проблемой занимались такие крупные физики, как Лоренц, Вин, Пуанкаре и другие, добиться удовлетворительного согласия с наблюдениями им не удалось[36].

Вальтер Ритц

Наибольший интерес вызвала «баллистическая теория» Вальтера Ритца (1908). В этой модели гравитационное взаимодействие осуществляют гипотетические частицы, которые, как надеялся Ритц, формируют также все электромагнитные явления. Формулу для силы автор выписал по аналогии с электродинамикой. Ритц скончался в возрасте 31 года (1909), не успев закончить развитие своей теории, но её оживлённое обсуждение продолжалось ещё десятилетие. В модели Ритца смещение перигелия для Меркурия, Венеры и Земли, а также перигея Луны было уже близко к реальным. Вместе с тем модель Ритца была несовместима с принципом постоянства скорости света и предсказывала несколько новых астрофизических эффектов, которые не подтвердились. В конечном счёте баллистическая теория не выдержала конкуренции с логически более безупречной и подтверждаемой опытом общей теорией относительности Эйнштейна (ОТО): например, отклонение света в гравитационном поле, предсказанное теорией Ритца, на четверть меньше эйнштейновского. В 1920-е годы интерес к теории Ритца угас[37].

Ещё одним конкурентом ОТО стала теория немецкого физика Пауля Гербера, опубликованная в 1898 году[38]. Исходя также из электродинамической аналогии, Гербер предложил формулу для гравитационного потенциала[39]:

V = μ r ( 1 − 1 c d r d t ) 2 , {\displaystyle V={\frac {\mu }{r\left(1-{\frac {1}{c}}{\frac {dr}{dt}}\right)^{2}}},}

где:

μ = 4 π 2 A 3 τ 2 {\displaystyle \mu ={\frac {4\pi ^{2}A^{3}}{\tau ^{2}}}} A {\displaystyle A} — большая полуось; τ {\displaystyle \tau } — период обращения.

Если скорость d r d t {\displaystyle {\frac {dr}{dt}}} мала по сравнению со скоростью света c {\displaystyle c} , то формула Гербера переходит в классическое выражение для гравитационного потенциала:

V = μ r {\displaystyle V={\frac {\mu }{r}}}

Из нового закона Гербер вывел ту же формулу для смещения перигелия Меркурия, что и в ОТО (см. ниже). Этот вывод и всё содержание теории Гербера подверглись критике со стороны многих видных физиков по нескольким причинам: произвольность ряда допущений, отсутствие лоренц-инвариантности, ошибочное значение для угла отклонения световых лучей в поле тяготения (в полтора раза выше эйнштейновского), дальнодействие и др.[39]Макс фон Лауэ в 1920 году писал, что «Гербер просто подогнал правильное его [численного коэффициента] значение, изменив соответственно без какого-либо физического обоснования математический подход своих двух предшественников» (В. Шайбнера и Ф. Тиссерана)[40].

Как заметил Н. Т. Роузвер, «ни одна из этих теорий не выдержала проверки на классических эффектах, подтверждающих общую теорию относительности, а измерения эффекта отклонения световых лучей явились для них камнем преткновения»[41].

Смещение перигелия Меркурия

Вулкан и вулканоиды

Предполагаемая орбита Вулкана (VULCAN) на схеме внутренних планет Солнечной системы

Вскоре после публикаций 1859 года французский астроном-любитель Эдмон Лескарбо (Edmond Modeste Lescarbault

Другие гипотетические объекты внутри орбиты Меркурия

Заниженная масса планет

Другие попытки объяснения

Гуго Ганс фон Зелигер в 1906 году исследовал гипотезу своего ученика, астронома Эрнста Андинга (Ernst Anding

Критика со стороны Саймона Ньюкома

Решение в рамках общей теории относительности[править | править код]

Альберт Эйнштейн, 1921
Основная статья: Задача Кеплера в общей теории относительности

После создания в 1905 году специальной теории относительности (СТО) А. Эйнштейн осознал необходимость разработки релятивистского варианта теории тяготения, поскольку уравнения Ньютона были несовместимы с преобразованиями Лоренца, а скорость распространения ньютоновской гравитации была бесконечна. В одном из писем 1907 года Эйнштейн сообщал[42]:

Сейчас я также занимаюсь исследованием закона тяготения с позиций теории относительности; надеюсь, это позволит мне пролить свет на ещё не объяснённое большое вековое смещение перигелия орбиты Меркурия.

Первые наброски релятивистской теории тяготения опубликовали в начале 1910-х годов Макс Абрахам, Гуннар Нордстрём и сам Эйнштейн. У Абрахама смещение перигелия Меркурия было втрое меньше реального, в теории Нордстрёма ошибочным было даже направление смещения, версия Эйнштейна 1912 года давала значение на треть меньше наблюдаемого[43].

В 1913 году Эйнштейн сделал решающий шаг — перешёл от скалярного гравитационного потенциала к тензорному представлению, этот аппарат позволил адекватно описать неевклидову метрику пространства-времени. В 1915 году Эйнштейн опубликовал окончательный вариант своей новой теории тяготения, получившей название «общая теория относительности» (ОТО). В ней, в отличие от ньютоновской модели, вблизи массивных тел геометрия пространства-времени заметно отличается от евклидовой, что приводит к отклонениям от классической траектории движения планет[43].

18 ноября 1915 года Эйнштейн рассчитал (приближённо) это отклонение[44] и получил практически точное совпадение с наблюдаемыми 43″ в столетие. При этом не понадобилось никакой подгонки констант и не делалось никаких произвольных допущений[45]. Если обозначить:

M {\displaystyle M} — масса Солнца;
c {\displaystyle c} — скорость света;
A {\displaystyle A} — величина большой полуоси орбиты планеты;
e {\displaystyle e} — эксцентриситет орбиты;
T {\displaystyle T} — период обращения,

то дополнительное смещение перигелия планеты (в радианах за оборот) в ОТО даётся формулой[46]:

δ φ ≈ 6 π G M c 2 A ( 1 − e 2 ) = 24 π 3 A 2 T 2 c 2 ( 1 − e 2 ) {\displaystyle \delta \varphi \ \approx \ {\frac {6\,\pi \,G\,M}{c^{2}\,A\,\left(1-e^{2}\right)}}\ =\ {\frac {24\,\pi ^{3}\,A^{2}}{T^{2}\,c^{2}\,\left(1-e^{2}\right)}}}

Для Меркурия эта формула даёт 42,98″ за столетие в отличном соответствии с наблюдениями. Точное решение уравнений Эйнштейна, полученное Карлом Шварцшильдом два месяца спустя (январь 1916, уже после открытия окончательной версии уравнений поля), подтвердило приведённую формулу.

До 1919 года, когда Артур Эддингтон обнаружил гравитационное отклонение света, объяснение смещения перигелия Меркурия было единственным экспериментальным подтверждением теории Эйнштейна. В 1916 году Гарольд Джеффрис выразил сомнение в адекватности ОТО, поскольку она не объясняла смещение узлов орбиты Венеры, ранее указанное Ньюкомом. В 1919 году Джеффрис снял свои возражения, поскольку, по новым данным, никаких аномалий в движении Венеры, которые не укладывались бы в теорию Эйнштейна, обнаружено не было[47].

Тем не менее критика ОТО продолжалась некоторое время и после 1919 года. Некоторые астрономы высказывали мнение, что совпадение теоретического и наблюдаемого смещения перигелия Меркурия может быть случайным, или оспаривали достоверность[47] наблюдаемого значения 43″. Современные точные измерения подтвердили оценки смещения перигелия планет и астероидов, предложенные ОТО[48][49].
Аномальная часть смещения перигелия, угловых секунд за столетие

Небесное тело	Теоретическое значение	Наблюдаемое значение
Меркурий	00043,0	0043,1 ± 0,5
Венера	00008,6	0008,4 ± 4,8
Земля	00003,8	0005,0 ± 1,2
Марс	00001,35	0001,1 ± 0,3
Икар (астероид)	00010,1	0009,8 ± 0,8

Большая погрешность данных для Венеры и Земли вызвана тем, что их орбиты почти круговые.

Формула ОТО была проверена также для двойной звезды-пульсара PSR B1913+16, в которой две звезды, по массе сравнимые с Солнцем, вращаются на близком расстоянии, и поэтому релятивистское смещение периастра каждой (аналога перигелия) очень велико. Наблюдения показали смещение на 4,2 градуса в год, в полном согласии с ОТО[50][51][52]. Самое большое смещение периастра обнаружено у открытого в 2003 году двойного пульсара PSR J0737−3039 — на 17 градусов в год; измерения 2005 года показали соответствие динамики системы предсказаниям ОТО с точностью 0,05 % в доверительном интервале 3 σ {\displaystyle 3\sigma } [53][54].

В 2020 году завершились более чем 30-летние измерения релятивистского смещения периастра для движения звезды вокруг компактного радиоисточника Стрелец A* (предположительно чёрной дыры) в центре нашей Галактики. Измерения проводил немецкий Институт внеземной физики Макса Планка. Результаты полностью соответствовали предсказаниям ОТО[55][56].

Прецессия перигелия небесных тел

Параметры орбит планет Солнечной системы из-за взаимовлияния этих планет со временем претерпевают медленные изменения. В частности, ось орбиты постепенно поворачивается (в плоскости орбиты) в сторону орбитального движения, соответственно, смещается и перигелий («прецессия перигелия», см. рисунок). Перигелий Меркурия возвращается в исходное положение каждые 260 тыс. земных лет, для Юпитера этот период составляет около 300 тыс. лет[3].

В середине XIX века астрономы обнаружили, что указанное смещение для Меркурия происходит несколько быстрее, чем предсказывает Закон всемирного тяготения, позже аналогичную аномалию обнаружили и в движении других небесных тел. Причина объясняется общей теорией относительности (ОТО); из уравнений ОТО вытекает именно такое значение смещения, которое наблюдается фактически. Добавочное смещение («релятивистская поправка») была посчитана и проверена для нескольких планет и астероидов[4][5]:

Небесное тело	Эксцентриситет орбиты	Добавочное смещение перигелия, угловые секунды за столетие
Небесное тело	Эксцентриситет орбиты	теоретическое	наблюдаемое
Меркурий	00000,205	00000043,0	00043,1 ± 0,5
Венера	00000,007	00000008,6	00008,4 ± 4,8
Земля	00000,017	00000003,8	00005,0 ± 1,2
Марс	00000,094	00000001,35	00001,1 ± 0,3
Икар (астероид)	00000,827	00000010,1	00009,8 ± 0.8

Большая погрешность данных для Венеры и Земли вызвана тем, что их орбиты почти круговые.

Примечания[править | править код]

Комментарии

Ранее «неправильное поведение» было отмечено у кометы Энке, видимо, из-за реактивной отдачи летучих веществ, и у Луны, см. Приливное ускорение, однако эти эффекты не вызывали сомнений в теории тяготения.

Источники

↑ 12
Роузвер Н. Т., 1985, с. 9—10.
Фейнман Р.
Характер физических законов. — Изд. 2-е. — М.: Наука, 1987. — С. 155. — 160 с. — (Библ. Квант, выпуск 62).
Субботин М. Ф., 1968, с. 65.
↑ 12
Роузвер Н. Т., 1985, с. 17.
Le Verrier U.
Théorie de mouvement de Mercure (фр.) // Ann. Observ. imp. — 1859. — Vol. 5, 1—96.
Le Verrier U.
Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète (фр.) // Comptes rendus hebdomadaires des séances de l’Académie des sciences. — 1859. — Vol. 49. — P. 379—383.
Clemence G. M.
The Relativity Effect in Planetary Motions (англ.) // Reviews of Modern Physics. — 1947. — Vol. 19. — P. 361—364. — doi:10.1103/RevModPhys.19.361.
↑ 123Isaac Asimov.
The Planet That Wasn’t (англ.) (May 1975). Дата обращения 6 мая 2014.
↑ 12Paul Schlyter.
Hypothetical Planets (англ.). Дата обращения 7 мая 2014.
Richard Baum, William Sheehan.
In Search of Planet Vulcan, The Ghost in Newton’s Clockwork Machine. — New York: Plenum Press, 1997. — ISBN 0-306-45567-6.
Роузвер Н. Т., 1985, с. 7—8, 33—36, 46, 61—62.
Роузвер Н. Т., 1985, с. 84—90, 97—117.
Субботин М. Ф., 1968, с. 61.
Роузвер Н. Т., 1985, с. 37—39, 60.
Роузвер Н. Т., 1985, с. 20—21, 31, 34, 47.
Роузвер Н. Т., 1985, с. 54—55, 59—60.
Hill H. A., Stebbins R. T.
The intrinsic visual oblateness of the sun // Astrophys. Journal. — 1975. — Вып. 200. — P. 471—483.
↑ 123
Визгин В. П., 1981, с. 36—37.
Гарцер П.
Звезды и пространство. // Новые идеи в математике. СПб.: Образование, 1913, вып. 3, с. 71—116.
Роузвер Н. Т., 1985, с. 98—116.
Newcomb S.
The elements of the four inner planets and the fundamental constants of astronomy. Suppl. am. Ephem. naut. Aim. 1897. U.S. Govt. Printing Office, Washington, D. C., 1895.
↑ 12
Роузвер Н. Т., 1985, с. 49—51, 57—58.
Роузвер Н. Т., 1985, с. 49—51, 57—63.
Богородский А. Ф., 1971, с. 35—58.
Роузвер Н. Т., 1985, с. 19.
Hall A.
A suggestion in the theory of Mercury (англ.) // Astr. J. — 1894. — Vol. 14. — P. 49—51.
Florin N. Diacu.
On the Mücket-Treder gravitational law // New Trends For Hamiltonian Systems And Celestial Mechanics / edited by Lacomba Ernesto A, Llibre Jaume. — 1996-07-03. — С. 127. — 407 с. — ISBN 9789814547901.
Гравитационный парадокс // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — ISBN 5-85270-034-7.
Роузвер Н. Т., 1985, с. 65—67.
Newcomb S.
Discussion and results of observations on transits Mercury from 1677 to 1881. Astr. Pap. am. Ephem. naut. Aim., t, 367—487. U. S Govt. Printing Office, Washington, D. C., 1882.
↑ 12
Роузвер Н. Т., 1985, с. 55—56.
Визгин В. П., 1981, с. 34—35.
Субботин М. Ф., 1968, с. 63.
Роузвер Н. Т., 1985, с. 8, 44, 82—83, 89—90.
↑ 12
Роузвер Н. Т., 1985, с. 139—161.
Визгин В. П., 1981, с. 44—49, 56—63.
Роузвер Н. Т., 1985, с. 161—168.
Gerber, P.
Die räumliche und zeitliche Ausbreitung der Gravitation // Zeitschrift für Mathematik und Physik. — 1898. — Vol. 43. — P. 93–104.
↑ 12
Роузвер Н. Т., 1985, с. 168—176.
Макс фон Лауэ.
О движении перигелия Меркурия (историко-критический очерк) // Лауэ М. Статьи и речи. — М.: Наука, 1969. — С. 86—89.
Роузвер Н. Т., 1985, с. 179.
Зелиг К.
Альберт Эйнштейн. — 2-е изд. — М.: Атомиздат, 1966. — С. 74.
↑ 12
Роузвер Н. Т., 1985, с. 180—186.
Эйнштейн А.
Объяснение движения перигелия Меркурия в общей теории относительности // Собрание научных трудов в 4 томах. — Т. I. — С. 439—447.
Пайс А.
Научная деятельность и жизнь Альберта Эйнштейна. — М.: Наука, 1989. — С. 245—248. — 568 с. — ISBN 5-02-014028-7.
Ландау Л. Д., Лифшиц Е. М.
Теория поля. — Издание 5-е, исправленное и дополненное. — М.: Наука, 1967. — 460 с. — («Теоретическая физика», том II)., § 98 «Движение в центрально-симметричном гравитационном поле».
↑ 12
Роузвер Н. Т., 1985, с. 113—117.
Kevin Brown.
Anomalous Precessions (англ.).
Reflections on Relativity
(2012). Дата обращения 14 апреля 2014.
Субботин М. Ф., 1968, с. 66.
Taylor J. H., Fowler L. A., McCulloch P. M.
Measurements of general relativistic effects in the binary pulsar PSR1913 + 16 (англ.) // Nature. — 1979. — No. 277. — P. 437.
The Binary Pulsar PSR 1913+16 (неопр.)
. Дата обращения 15 апреля 2014.
Нарликар Дж.
Гравитация без формул. — М.: Мир, 1985. — С. 88. — Тираж 50 000 экз.
M. Kramer et al.
Tests of General Relativity from Timing the Double Pulsar (англ.) // Science. — 2006. — 6 October (vol. 314, iss. 5796). — P. 97—102. — doi:10.1126/science.1132305.
Robert Naeye.
Einstein Passes New Tests.
(Collective of authors GRAVITY Collaboration).
Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole // Astronomy & Astrophysics. — 2020. — Т. 636.
Телескоп ESO наблюдает «звездный танец» вокруг сверхмассивной чёрной дыры и подтверждает правоту Эйнштейна (неопр.)
. European Southern Observatory.
Лев Окунь
. Основные понятия и законы физики и свойства элементарных частиц материи // Доклад на Президиуме РАН 27 октября 2009 г. -Элементы.ру

Смульский Составляющие прецессии перигелия Меркурия

Смульский

Институт Криосферы Земли СО РАН, г. Тюмень

Я посмотрел представленную на Wiki site таблицу (см. табл. 1) (https://en. wikipedia. org/wiki/Tests_of_general_relativity). Её данные мне хорошо известны. Составляющие прецессии, т. е. вращения перигелия Меркурия на Wiki site, как и в современной физике, даны неверно. Вот уже 100 лет физики-теоретики по незнанию вводят читателя в заблуждение. Поэтому, если уж представлять на Wiki site объяснение этому явлению, то нужно давать его во всех деталях.

Табл. 1. Wiki site table at https://en. wikipedia. org/wiki/Tests_of_general_relativity.

Sources of the precession of perihelion for Mercury
Amount (arcsec/Julian century)	Cause
5028.83 ±0.04 [4]	Coordinate (due to the precession of the equinoxes)
530[5]	Gravitational tugs of the other planets
0.0254	Oblateness of the Sun (quadrupole moment)
42.98 ±0.04 [6][7]	General relativity
5603.24	Total
5599.7	Observed
-3%)	Discrepancy

Вращение перигелия Меркурия можно определить в результате анализа изменений нескольких параметров орбит планет. Для этого рассмотрим, какие изменения происходят с орбитами планет и с точками, от которых осуществляется отсчет углов. На рис. 1 в гелиоцентрической экваториальной системе координат xyz
плоскость орбиты планеты (Меркурия) прочерчивает на небесной сфере дугу окружности
DAB
, а проекция перигелия орбиты отмечена точкой
B
. Неподвижные плоскости экватора
A0A0‘
и эклиптики
E0E0‘
зафиксированы на определенную эпоху, например, 1950.0 г. или 2000.0 г. Остальные плоскости экватора
AA‘
, эклиптики
EE‘
и орбиты Меркурия
DAB
в эпоху
Т
движутся в пространстве.

Рис. 1. Основные плоскости на небесной сфере C

:
A0A0‘–
неподвижная плоскость экватора Земли на 1950.0 г.;
E0E0‘–
неподвижная плоскость орбиты Земли на 1950.0 г. (плоскость неподвижной эклиптики);
AA‘–
подвижная плоскость экватора Земли в эпоху
Т
;
EE‘–
подвижная плоскость орбиты Земли в эпоху
Т
(наклон для наглядности увеличен);
g0–
точка весеннего равноденствия 1950.0 г.;
g–
точка на линии пересечения подвижного экватора в эпоху
Т
с подвижной эклиптикой (точка весеннего равноденствия в эпоху
Т)
;
DAB–
плоскость орбиты Меркурия в эпоху
Т
.

Углы между плоскостями представлены на рис. 2, соответствует рис. 2б нашей работы [1], в которой результаты приведены для Марса, но они справедливы для любой планеты, включая Меркурий. Так как плоскости экватора Земли AA

‘ и орбиты Земли
EE
‘ на рис. 2 перемещаются со временем в пространстве, поэтому точка весеннего равноденствия
g
удаляется по дуге
g
2
g
от плоскости неподвижного экватора
A
0
A
0′ со скоростью

= 5025².641 + 2².223
Tt,
(1)

где pc

– скорость в arcsec/столетие,
Tt
– время в тропических столетиях от эпохи 1900.0 г. Следует отметить, что в геоцентрической системе точку
g
Солнце проходит весной, а в гелиоцентрической системе точку
g
Земля проходит осенью.

Формула (1) получена С. Ньюкомбом [2] в результате аппроксимации данных наблюдения на интервале нескольких сот лет. Она даёт скорость удаления точки g

от неподвижной плоскости экватора
A
0
A
0′ равную -5026.75 arcsec/столетие для 1950.0 г. и -5027.86 arcsec/столетие для 2000.0 г. Так как точка
g
движется за стрелкой часов, поэтому скорость записана со знаком «-».

В астрономии перемещение точки перигелия B

определяют долготой
pa
, которую в результате аппроксимации данных наблюдения С. Ньюкомб [2] представляет в виде полинома третьей степени от времени:

πa

= 334○13¢05².53 + 6626².73·
Tj
+ 0².4675·
Tj
2 – 0².0043·
Tj3
, (2)

где Tj

– время, отсчитываемое в юлианских столетиях по 36525 суток от фундаментальной эпохи 1900.0.

Величина pa

представляет собой сумму двух разных дуг (см. рис. 2)

πa

=
gA+AB
, (3)

где дуга gA

=
Wa
называется долготой восходящего узла орбиты Меркурия.

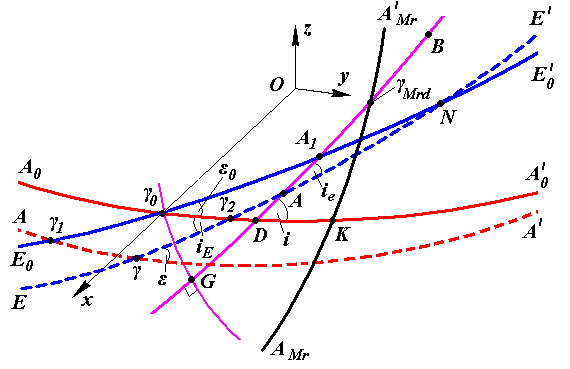
Рис. 2. Составляющие части вращения перигелия Меркурия на небесной сфере. Обозначения плоскостей дано на рис. 1; g0G
–
дуга большого круга, перпендикулярного плоскости орбиты Меркурия
GDAB
;
B –
гелиоцентрическая проекция перигелия Меркурия на небесной сфере;
А–
восходящий узел орбиты Меркурия на подвижной эклиптике;
D–
восходящий узел орбиты Меркурия на неподвижном экваторе 1950 г.; параметры орбиты Меркурия в инерциальной экваториальной системе координат:
jW
=
g0D
;
jр
.=
DB
;
i
= Ð
g0DG
;
iE
– наклон подвижной орбиты Земли (подвижной эклиптики); и в подвижной эклиптической системе:
Ωa
=
gA
;
ωa
=
AB
;
πa
=
gA+AB
=
Ωa
+
ωa
;
iеа
=
iе
= Ð
gAG
; индекс «
e
» – углы по отношению к подвижной эклиптике; индекс «
a
» – по результатам аппроксимации данных наблюдения.

Из формулы (2) скорость вращения перигелия по пути дуг gA

+
AB
равна 5602.9 arcsec/столетие для 1950.0 г. и 5601.9 arcsec/столетие для 2000.0 г. Из рис. 2 видно, что при определении точки перигелия
B
величиной
pa
, в скорость перемещения перигелия войдут: 1) скорости движения точки
g
по подвижной эклиптике
EE
‘; 2) скорость смещения точки
A
подвижной эклиптики
EE
‘ за счёт её вращения вокруг т.
N
и 3) скорость смещения восходящего узла
A
орбиты Меркурия
GDAB
по подвижной эклиптике
EE‘
, вызванного вращением плоскости
GDAB
. Чтобы эти скорости не оказывали влияния на скорость движения перигелия, необходимо ее отсчитывать от неподвижной точки. В качестве такой точки я взял точку
G
, которая находится на пересечении круга
GDAB
с перпендикулярным к ней кругом
g0G
. В работе [1] я вывел формулу (29) для дуги
GB
, которая зависит от параметров подвижных плоскостей орбит Земли (
EE
‘) и Меркурия (
GDAB
) и имеет следующий вид:

jp0a

=
GB=pa—Wа
+ arcsin[sin
iEa
sin
(Wа—gg2)/
sin
iа
] +

+ arccos[cos jWa/(1 — (

sin
jWa
sin
iа)2)0.5
]. (4)

Обозначения величин приведены в подрисуночной подписи к рис. 2. Для углов jWa

и
iEa
в работе [1] приведены также формулы в зависимости от эклиптических углов орбит:
Ωa
,
iеа
и др. В результате аппроксимации данных наблюдения С. Ньюкомб [2] представил эклиптические углы в виде полиномов третьей степени по времени, примером которой является формула (2). Дж. Л. Симон и др. [3] результаты С. Ньюкомба привели к 2000.0 г. и представили в виде полиномов 6-ой степени.

Формула (4) даёт скорость вращения перигелия орбиты Меркурия относительно неподвижного пространства равную 582.05 arcsec/столетие для 1950.0 г. и 583.15 для 2000.0 г. [4]. Это скорость вращения перигелия по данным наблюдения. По параметрам Дж. Л. Симона и др. [3] она равна 582.53 arcsec/столетие для 2000.0 г.

Взаимодействие тел Солнечной системы по закону тяготения Ньютона приводит к изменению их орбит, в том числе к вращению перигелиев. Если рассматривать тела как материальные точки, то скорость движения перигелия Меркурия относительно неподвижной точки G

на рис. 2 равна 529.86 arcsec/столетие [4], т. е. меньше на 52÷53 arcsec/столетие от наблюдаемой величины.

Для выяснения причины отличия рассчитанной по ньютоновскому взаимодействию и по данным наблюдения скорости вращения перигелия Меркурия я провел разнообразные исследования. Во-первых, я установил, что такое отличие скорости вращения перигелия имеется только для Меркурия, самой близкой планеты к Солнцу. Во-вторых, рассчитанные по взаимодействию Ньютона другие параметры орбиты Меркурия и скорости их изменения практически совпадали с данными наблюдения [4].

Я исследовал влияние скорости тяготения на результаты взаимодействия двух тел. Общая теория относительности (ОТО) была создана для того, чтобы учесть конечную скорость тяготения. А. Эйнштейн основал её на уравнениях и результатах Пауля Гербера. Пауль Гербер придумал такой механизм распространения тяготения со скоростью света, чтобы он объяснял вращение перигелия величиной 43 arcsec/столетие [5]. Однако, как я показал в статье [4], этот механизм ничем не обоснован и является ошибочным. Кроме того, как показано выше, отличие расчетов по ньютоновскому взаимодействию и наблюдениями равно не 43 arcsec/столетие, а 52÷53 arcsec/столетие.

В природе известен только один механизм распространения воздействия со скоростью света – это механизм распространения электромагнитного воздействия. Из экспериментальных законов электромагнетизма я вывел выражения для силы взаимодействия двух наэлектризованных частиц [6]:

, (5)

где k = ke = q1 q2/ε

, ,
r
и
v
– расстояние и скорость одной частицы относительно другой;
q1
и
q2
– заряды частиц;
ε
– диэлектрическая проницаемость среды между частицами, а
c1
– скорость света в ней.

Как видно из (5), при не мгновенном взаимодействии сила зависит не только от расстояния между частицами r

, но и от их относительной скорости
v
. Если для тяготения принять такой же механизм распространения воздействия, то формулой (5) будет определяться сила тяготения при
k = kG= —G·m1·m2
, где
m1
и
m2
– массы взаимодействующих тел, а
G
– гравитационная постоянная. С силой я рассчитал траекторию движения одного тела относительно другого при всех возможных изменениях эксцентриситета и скорости тела в перигелии [7]-[9]. В случае эллиптической орбиты перигелий вращается и тем сильнее, чем больше скорость тела в перигелии. В такой орбите изменяется длина большой полуоси и период обращения по сравнению с орбитой, полученной при взаимодействии двух тел по закону тяготения Ньютона. Изменения полуоси и периода имеют такой же порядок как изменения угла перигелия.

Получить полный текст

Расчет вращения перигелия Меркурия при силе дал величину скорости 0.23 arcsec/столетие [7], т. е. почти в 200 раз меньшую величину, чем объясняемая Паулем Гербером величина 43 arcsec/столетие [5] и принятая в ОТО. Отсюда следуют, что излишек вращения перигелия в 52÷53 arcsec/столетие не может объясняться механизмом распространения тяготения со скоростью света.

Объяснение излишка вращения перигелия сплюснутостью Солнца в настоящее время затруднено сложностями модели взаимодействия и отсутствием знаний о распределении плотности Солнца по радиусу и вдоль оси Солнца. Поэтому выполненные расчеты влияния сплюснутости Солнца, по всей видимости, являются недостоверными.

Табл. 2. Скорость вращения перигелия Меркурия по наблюдениям и по ньютоновскому взаимодействию. Для сравнения в скобках – по данным Wiki site.

Количество (arcsec/столетие)	Объяснение
По данным наблюдения
-5027.86 – Ncb -5028.82– Sim (5028.83 – Wiki site)	Скорость движения точки весеннего равноденствия g относительно неподвижного пространства (по форм. (1))
5601.9 – Ncb 5603.0 – Sim (5599.7 – Wiki site)	Скорость вращения перигелия от подвижной точки g весеннего равноденствия с включением скоростей изменения эклиптики и орбиты Меркурия (по форм. (2))
583.15 – Ncb 582.53 – Sim	Скорость вращения перигелия относительно неподвижного пространства (по форм. (4))
По результатам взаимодействия по закону тяготения Ньютона. Скорость вращения перигелия относительно неподвижного пространства
530 (530– Wiki site)	Планеты и Солнце взаимодействуют как материальные точки
582	Планеты взаимодействуют как материальные точки, а сплюснутость и вращение Солнца учитывается в виде составной модели

Если бы внутри орбиты Меркурия находилась планета определенной массы, то она могла бы произвести необходимое вращение перигелия Меркурия и в то же время не оказать заметного влияния на другие планеты. Такой планеты нет. Но Солнце вращается вокруг своей оси, и движущиеся массы его вещества могут воздействовать на Меркурий так же, как и предложенная выше планета. Я разработал составную модель вращения Солнца [4] и рассмотрел различные варианты ее воздействия по закону тяготения Ньютона совместно с воздействием остальных тел Солнечной системы. Оказалось, что при определенной массе периферийных тел модели может быть получена такая же скорость вращения перигелия как наблюдаемая, т. е. 582 arcsec/столетие. При этом скорость изменения остальных параметров орбиты Меркурия существенно не изменяется. Существенно не изменяется также скорость перигелия Венеры, а параметры планет более удаленных от Солнца изменяются еще в меньшей степени. Отметим, что составная модель вращения Солнца учитывает сплюснутость Солнца и вращение его масс.

Узнай стоимость своей работы

Бесплатная оценка заказа!

В результате проведенных исследований запишем основные характеристики вращения перигелия Меркурия в таком виде, чтобы их можно было сопоставить с данными на Wiki site (см. Табл. 2). Результаты по данным наблюдения мы приводим для 2000.0 г. по элементам орбит С. Ньюкомба [2] (Ncb) и Дж. Л. Симона и др [3] (Sim).

Литература

1. Grebenikov E. A., Smulsky J. J. Evolution of the Mars Orbit on Time Span in Hundred Millions Years / Reports on Applied ssian Academy of Sciences: A. A. Dorodnicyn Computing Center. Moscowp.(In Russian).

2. Newcomb S. The elements of the fourth inner planets and the fundamental constants of astronomy. Washington: Government printing office. 1895. –202 p.

3. Simon J. L., Bretagnon P., Chapront J. et al. Numerical Expression for Precession Formulae and Mean Elements for the Moon and the Planets // Astron. Astrophys. – 1994, vol. 282, p. 663-683.

4. Smulsky J. J.Gravitation, Field and Rotation of Mercury Perihelion// Proceedings of the Natural Philosophy Alliance. 15th Annual Conference 7-11 April 2008 at the University of New Mexiko, Albuquuerque, USA. Vol. 5, No. 2. Published by Space Time Analyses, Ltd. Arlington, MA, USA.– 2009. – Pp. 254-260.

5. Gerber P. Die raumliche und zeitliche Aubreitung der Gravitation// Z. Math. Phis.- 1898.- Vol. 43.- P. 93-104. https://bourabai. /articles/gerber/gerber. htm. (Tanslated into Russian by Johann Kern).

6. Smulsky, J. J. 1994. «The New Approach and Superluminal Particle Production», Physics Essays. — Vol. 7. — No. 2. — P.

7. Smulsky, J. J. The Theory of Interaction. — Ekaterinburg, Russia: Publishing house «Cultural Information Bank», 20p. (In English)

8. Smulsky J. J. The new Fundamental Trajectories: part 1 — Hyperbolic/Elliptic trajectories//Galilcan Electrodynamics. Vol. 13, No. 2, 2002, pp. 23-28.

9. Smulsky J. J. The new Fundamental Trajectories: part 2 — Parabolic/ Elliptic trajectories// Galilcan Electrodynamics. Vol. 13, No. 3, 2002, pp. 47-51.

31/10/2010 г.

Литература[править | править код]

Богородский А. Ф.
Всемирное тяготения. — Киев: Наукова думка, 1971. — 351 с.
Визгин В. П.
Релятивистская теория тяготения. Истоки и формирование. 1900—1915 гг. — М.: Наука, 1981. — 352 с.
Климишин И. А.
Релятивистская астрономия. — 2-е изд. — М.: Наука, 1989. — С. 35—41. — ISBN 5-02-014074-0.
Роузвер Н. Т.
Перигелий Меркурия. От Леверье до Эйнштейна = Mercury’s perihelion. From Le Verrier to Einstein. — М.: Мир, 1985. — 244 с.
Спасский Б. И.
История физики, в двух томах. — М.: Высшая школа, 1977.
Субботин М. Ф.
Введение в теоретическую астрономию. — М.: Наука, 1968. — С. 58—67.
Earman J., Janssen M.
Einstein’s Explanation of the Motion of Mercury’s Perihelion // The Attraction of Gravitation: New Studies in the History of General Relativity: Einstein Studies, Volume 5. — Boston: Birkhãuser, 1993. — С. 129—149. — 432 с. — ISBN 3764336242.