Со́лнечные су́тки
— промежуток времени, за который небесное тело совершает 1 поворот вокруг своей оси относительно центра Солнца.[
уточнить
]
Более строго это промежуток времени между двумя одноимёнными (верхними или нижними) кульминациями (прохождениями через меридиан) центра Солнца в данной точке Земли (или иного небесного тела).
Солнечные сутки на Земле
Колебания продолжительности солнечных суток
Из-за эллиптичности земной орбиты линейная скорость движения и угловая скорость вращения Земли вокруг Солнца изменяется в течение года. Медленнее всего Земля движется по орбите, находясь в афелии — самой удалённой от Солнца точке орбиты, быстрее всего — находясь в перигелии. Это является существенной причиной изменения длительности солнечных суток в течение года. А наклон приводит к движению Солнца по небесной сфере вверх и вниз от экватора в течение года. При этом прямое восхождение Солнца вблизи равноденствий изменяется быстрее (так как скорость склонения Солнца максимальна и складывается с постоянной экваториальнй скоростью), чем во время солнцестояний, когда скорость склонения меняет направление, следовательно равна нулю, когда оно движется параллельно экватору.
Вклад эллиптичности орбиты в колебание длительности солнечных суток можно описать синусоидой с амплитудой +7,931 секунд в перигелии и −7,92 секунд в афелии с периодом в 1 год. Есть и другие периодические эффекты, вносящие вклад в длину солнечных суток и зависящие от времени, но они невелики (возмущения от Луны и планет и т. д.).
Колебание продолжительности солнечных суток приводит к тому, что истинное солнечное время также колеблется относительно среднего солнечного времени. А именно: в результате накопления отклонений продолжительности солнечных суток от 24 часов солнечные часы спешат или отстают в зависимости от момента отсчёта. А, именно: если начать с осени, когда амплитуда колебания проходит через значение нуль, это на 13 суток позже дня осеннего равноденствия, а затем достигает выше упомянутого максимума +7,931 секунды, это 4 января, когда Земля проходит точку перигелия, и до весны, когда амплитуда опять проходит нулевое значение, это позже дня весеннего равноденствия на также 13 суток, отставание составит с использованием интегрального исчисления S = 7,931*180*2/π = 908,82565463651 с = 15 мин. 8,825.. сек. Теперь, если полученную сумму разделим пополам, получим положительную амплитуду уравнения времени, обусловленную эллиптичностью орбиты, равную 7 минутам и 34,41 секунды (см. Истинная механика движения Земли вокруг Солнца и формула истинных солнечных суток).
Средние солнечные сутки
Чтобы не учитывать эту переменность в повседневной жизни, используют средние солнечные сутки
, привязанные к так называемому
среднему Солнцу
— условной точке, движущейся равномерно по небесному экватору (а не по эклиптике, как реальное Солнце) и совпадающей с центром Солнца в момент весеннего равноденствия. Период обращения среднего Солнца по небесной сфере равен тропическому году.
Средние солнечные сутки не подвержены периодическим
изменениям, как истинные солнечные сутки, но их длительность монотонно изменяется в связи с изменением периода осевого вращения Земли и (в меньшей степени) с изменением длительности тропического года, увеличиваясь примерно на 0,0017 секунды в столетие. Так, длительность средних солнечных суток в начале 2000 года была равна 86400,002 секунды . Следует отметить, что здесь в качестве единицы измерения указана именно секунда СИ, определённая с использованием внутриатомного периодического процесса, а не средняя солнечная секунда, которая по определению равна 1/86 400 части средних солнечных суток и, следовательно, также не является постоянной.
Введение поправок
Хотя средние солнечные сутки не являются, строго говоря, неизменной единицей времени, но повседневная жизнь людей связана именно с ними. В связи с накоплением поправки к длительности суток в среднем солнечном времени по отношению к равномерному атомному времени, иногда приходится добавлять к атомной шкале UTC так называемую високосную секунду, чтобы восстановить привязку этой шкалы к солнечной шкале времени . Теоретически возможно и вычитание високосной секунды, так как вращение Земли в принципе не обязано постоянно замедляться.
Единицы измерения времени
Наблюдение и измерение времени основано на обращении нашей планеты вокруг Солнца.
Время, которое прошло можно измерить исходя из следующих моментов.
Земля вокруг своей оси движется почти равномерно. Период этого движения равен периоду вращения небесного свода. В свою очередь период вращения небесного свода может быть определен из наблюдений за ним.
Таким образом, исходя из знания об угле поворота Земли от некоего начального положения можно сделать расчет прошедшего времени.
При этом за начальное положение Земли принимаются следующие моменты.
- момент прохождения нашей планеты через выбранную точку на небе
- момент верхней или нижней точки кульминации на выбранном меридиане.
Замечание 1
Основной единицей времени являются сутки. Их продолжительность зависит от выбранной точки на небе.
Такими точками являются:
- точка весеннего равноденствия
- центр видимого диска Солнца (истинное Солнце)
- среднее солнце – некая умозрительная точка, расположение которой может быть определено теоретически и для любого момента времени.
Готовые работы на аналогичную тему
- Курсовая работа Время в астрономии 490 руб.
- Реферат Время в астрономии 220 руб.
- Контрольная работа Время в астрономии 250 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Данные точки действуют для трех единиц времени, а именно:
- звездные сутки
- истинные солнечные сутки
- средние солнечные сутки
Время, которое при этом измеряется, соответственно называется звездное время, истинное солнечное, и среднее солнечное.
Звездные сутки.
Звездными сутками называется отрезок прошедшего времени, который был зафиксирован между двумя последовательными одноименными кульминациями точки весеннего равноденствия, которые были отмечены на одном и том же меридиане.
При этом за начало звездных суток на выбранном меридиане принимается момент верхней кульминации точки весеннего равноденствия.
Звездное время.
Звездным временем называют время, которое прошло с момента верхней кульминации точки весеннего равноденствия до любого иного её положения. Это время определяется в звездных часах, минутах и секундах.
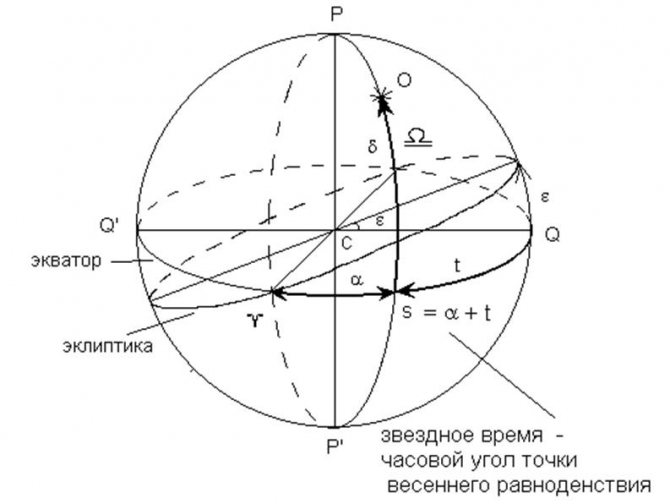

Рисунок 1. Звездное время. Автор24 — интернет-биржа студенческих работ
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут!
Задать вопрос
Замечание 2
Пользование звездным временем удобно лишь в научных астрономических расчетах. В быту пользование такими расчетами неудобно. В частности, из-за того, что солнце лишь раз в году проходит точку кульминации весеннего равноденствия, в дальнейшем полдень наступает в различное время суток, что создает неудобство.
Истинные солнечные сутки.
Под этим термином понимается последовательность одноименных кульминаций Солнца, а если быть более точным, то центра солнечного диска на не меняющемся географическом меридиане. При этом началом истинных солнечных суток является момент нижней кульминации Солнца, что также называют истинной полночью.
Истинное солнечное время.
Определение 1
Под истинным солнечным временем $T$ понимается такое время, которое истекло после нижней кульминации нашего светила до любого иного его положения.
При этом, данное положение выражается в отрезках времени истинных солнечных суток, таких как истинные солнечные часы, минуты и секунды.
В результате истинное солнечное время $T$ на выбранном меридиане в искомый момент равняется часовому углу Солнца $t$. В свою очередь часовой угол Солнца $t$ определяется в часовой мере плюс $12h$.
В результате получается следующая формула:
$T¤ = t¤ + 12h$
Также следует сказать, что движение по небосклону истинного Солнца не равномерно в силу следующих причин:
Наше светило идет по эклиптике, а не по небесному экватору. Эклиптика наклонена к небесному экватору под углом = 23°27 Солнце движется по эклиптике неравномерно.
В силу данных причин истинные солнечные сутки в один день года могут быть больше чем в другой, или меньше. Поэтому из-за постоянного изменения длительности истинных солнечных суток применять их для отсчета времени в реальной жизни не представляется возможным.
Средние солнечные сутки.
Для получения суток постоянной длительности, взаимосвязанных с ходом Солнца, были введены следующие понятия.
Среднее эклиптическое и среднее экваториальное солнце – фиктивные точки, используемые астрономами для получения суток, которые отличались бы постоянной длительностью и были связаны с ходом Солнца.
Среднее эклиптическое солнце, двигается по эклиптике со среднею скоростью нашего светила. 3 июля и 4 января среднее эклиптическое солнце совпадает с реальным.
В свою очередь среднее экваториальное солнце идет по небесному экватору с постоянной скоростью, которая есть у среднего эклиптического солнца. Эклиптическое и экваториальное солнце одновременно проходят точку весеннего равноденствия.
Средние (солнечные) сутки – данным термином называется определенный промежуток времени между двумя последовательными кульминациями среднего экваториального солнца.
Замечание 3
При этом началом средних экваториальных суток считается момент, когда среднее экваториальное солнце достигает нижней своей кульминации. Этот момент так же называется средней полночью.
Среднее время $Tm$ – промежуток, который прошел от момента, когда произошла нижняя кульминация среднего экваториального солнца до любого иного положения солнца. При этом данное положение выражается в долях средних солнечных суток, а именно в средних часах, минутах и секундах.
В результате среднее время $Tm$ рассчитывается исходя из того, что оно равно численно в любой момент на нужном меридиане часовому углу $tm$ среднего экваториального солнца. В свою очередь часовой угол среднего экваториального солнца определяется в часовой мере $12h$.
В результате получаем такую формулу:
$Tm = tm +12h$.
Солнечные сутки на других планетах и спутниках
Луна
Средние солнечные сутки на Луне равны среднему синодическому месяцу (среднему промежутку между двумя одинаковыми фазами Луны, например, полнолуниями) — 29 суток 12 часов 44 минуты 2,82 секунды. Истинные солнечные сутки могут отклоняться от средних на 13 часов в обе стороны, что связано как с неравномерностью движения Земли по орбите, так и с наклоном орбиты Луны к эклиптике, с эллиптичностью её орбиты и с наклоном оси вращения Луны к плоскости орбиты (см. также Либрация).
Другие спутники планет
Как и в случае Луны, большинство спутников планет в Солнечной системе вследствие приливного резонанса имеют орбитальный период, равный периоду осевого вращения. Таким образом, для этих спутников средние солнечные сутки близки к периоду обращения вокруг планеты. Исключениями являются самые внешние спутники планет-гигантов (например, Феба), а также Гиперион, который вращается вокруг своей оси хаотически.
Планеты
На газовых гигантах, не имеющих твёрдой поверхности, солнечные сутки зависят от широты — атмосфера вращается с разными скоростями на разных широтах.
Меркурий обходит вокруг Солнца за 87,97 дня, а вокруг своей оси делает полный оборот за 58,65 дня (эти периоды относятся как 3:2). Средний промежуток времени между двумя верхними кульминациями Солнца на этой планете равен 176 дням, что равно двум её годам. Интересно, что когда он находится вблизи перигелия, Солнце для наблюдателя на поверхности планеты может в течение 8 дней двигаться в обратном направлении, поэтому, строго говоря, привязка определения солнечных суток к кульминации в этом случае не вполне корректна.
На Венере, чей сидерический период обращения вокруг своей оси равен 243 дням — больше, чем орбитальный период (224,7 дня), средние солнечные сутки равны примерно 116,7 дня (из-за вращения в обратную сторону)
На Марсе средние солнечные сутки лишь слегка больше, чем земные. Они равны 24 ч 39 мин 35,244 с.
На Юпитере сутки равны 9 часам 55 минутам 40 секундам, на Сатурне 10 часам 34 минутам 13 секундам. Сутки на Уране равны 17 часам 14 минутам 24 секундам, а на Нептуне 15 часам 57 минутам 59 секундам.
У Плутона ввиду его крайней удалённости от Солнца (и, следовательно, малости угловой орбитальной скорости) средние солнечные сутки практически равны периоду вращения: 6 дней 9 часов 17 минут 36 секунд.
О солнечных календарях
А.А.Дмитриевский
Скоро Новый год.
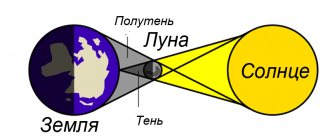
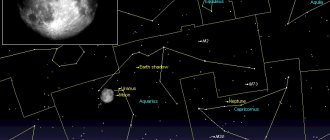
А завтра, 21 декабря будет полное лунное затмение, которое в России можно видеть только на северо-востоке России.
Поэтому я решил написать о солнечных календарях.
Слово «календарь» в русском языке имеет много значений. Здесь под словом «календарь» понимается система измерения и счета длительных промежутков времени, значительно более длинных, чем сутки.
Теория солнечных календарей — очень проста для понимания. И оказывается, что эта теория, несмотря на то, что является довольно абстрактной, имеет прямое отношение к практике исчисления времени для целей богослужения. Поэтому она и стала ареной борьбы различных направлений христианства.
Люди, пытаясь обосновать свои предпочтения (какой календарь лучше, юлианский или григорианский календарь), тщетно стремятся доказать недоказуемое.
Я воздержусь от того, чтобы погружаться в полемику с религиозной окраской, тем более, что по этому поводу понаписано много глупостей с точки зрения астрономии, и самое разумное — все игнорировать.
Моя цель: объяснить простым человеческим языком теорию солнечных календарей, без излишних усложнений, — только самое необходимое.
1. Почему есть те или иные календари?
Сорок с лишним лет тому назад я вместе с другими студентами, обучающимися на военной кафедре, был на военных сборах целых два месяца. У нас не было ни газет, ни радио, нам не нужно было знать какое сегодня число. Каждое утро подъем, делаешь, что приказано, а вечером отбой. И так день за днём….
Я с удивлением заметил, что стал считать время по Луне! Например: «В лагерях мы должны быть две луны. Полторы луны уже прошло, значит осталось половина луны, — около двух недель».
Оказывается, очень удобно ориентироваться во времени по фазам Луны! Неудивительно, что весь мусульманский мир живёт по лунному календарю. Такой календарь имеет своим истоком быт скотоводов и кочевников.
Дата в лунном календаре указывает на фазу Луны.
Земледельцем фаза Луны не очень интересна. Им важно провести сельхозработы в благоприятное для этого время. Ориентироваться по погоде получается не всегда, — год на год, как мы знаем, не приходится. Поэтому земледельцам нужен календарь, который указывал бы на сезон года.
В свою очередь, сезоны года зависят от Солнца: летом Солнце высоко над горизонтом, да и дни длиннее, поэтому летом тепло. Зимой всё наоборот.
Поэтому для земледельцев солнечный календарь — самый подходящий.
Кроме того, солнечный календарь предпочтительнее, чем лунный в умеренных поясах Земли, потому что именно там наиболее выражены сезоны года.
Дата в солнечном календаре указывает на сезон года.
Итак, в практике всех народов мира применяются, в основном, два типа календарей, — лунные и солнечные.
Другие типы календарей — экзотика.
В частности, лунно-солнечные календари, указывающие и на фазу Луны, и на сезон года, слишком сложны, поэтому широкого распространения не получили.
2. Что такое средние солнечные сутки?
Прежде чем вести учёт длительных промежутков времени, нужно определиться, в каких единицах это делается.
Наша обыденная жизнь связана со световым днём и, следовательно, с Солнцем. Поэтому естественно было бы взять за основу истинное солнечное время, которое показывают солнечные часы. А промежутки времени измерять в истинных солнечных сутках, которые длятся от одного полудня, когда Солнце выше всего над горизонтом, до следующего, когда оно снова будет выше всего над горизонтом.
Но, оказывается, не так всё просто. Уже более трёхсот лет тому назад парижские часовщики написали на цеховом гербе: «Солнце показывает время обманчиво». — Показания солнечных и точных механических часов расходятся, причём разница может превышать 16 минут. Это значит, что истинное солнечное время — не равномерное, а истинные солнечные сутки имеют разную продолжительность в зависимости от сезона года.
Отсюда понятно, что для точного измерения и счёта времени истинное солнечное время и истинные солнечные сутки не подходят; требуется равномерно текущее время с одинаковыми по длительности сутками, и, кроме того, имеющее привязку к Солнцу.
Следовательно, истинное солнечное время нужно исправить. Для этого вводят поправку, называемую уравнением времени, — число минут, секунд и долей секунд, которые прибавляют к истинному солнечному времени, чтобы получить равномерно текущее среднее солнечное время.
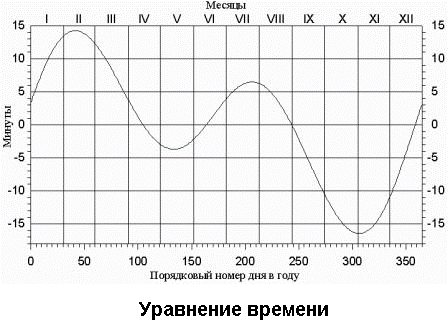

Средние солнечные сутки (это промежуток времени от 0 часов среднего солнечного времени до следующего 0 часов) всегда имеют одинаковую продолжительность.
Именно средними солнечными сутками мы пользуемся в обыденной жизни. Когда мы говорим, что прошло столько-то суток, это означает, что речь идёт как раз о средних солнечных сутках.
Длительные промежутки времени в сутках измерять неудобно. Например, если вы спросите меня, каков мой возраст, я отвечу: примерно 22300 суток, — получается слишком большое число. Такими числами неудобно оперировать, они не обладают наглядностью. Поэтому все мы пользуемся тем или иным календарём, — системой измерения и счёта длительных промежутков времени.
3. Как установить тот факт, что Земля совершила полный оборот по отношению к Солнцу?
Нам уже известно, что дата в солнечном календаре указывает на сезон года. Чтобы календарь был точным, нужно чтобы продолжительность календарного года была бы в точности равна периоду, с которым меняются сезоны года.
Поэтому требуется знать период, с которым меняются сезоны года.
В начальной школе учили, что сезоны года меняются потому, что Земля совершает полный оборот вокруг Солнца за один год. Следовательно, сезоны года меняются с таким же периодом. Это совершенно правильный ответ. Но очень не точный, он нас не устраивает.
Поэтому поставим вопрос немного по-другому: «Что значит полный оборот, т.е. как установить тот факт, что Земля совершила полный оборот вокруг Солнца?»
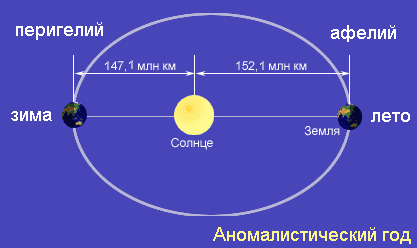
Может быть так? — В какой-то момент Земля была ближе всего к Солнцу (в перигелии своей орбиты, это бывает в первых числах января), потом сделала полный оборот и снова вернулась туда же? Соответствующий промежуток времени астрономы называют аномалистическим годом. Его продолжительность равна 365,2596 средних солнечных суток.

А может быть по-другому? Если бы мы находились среди далёких звёзд, т.е. смотрели на солнечную систему со стороны, то обнаружили бы, что Земля обращается вокруг Солнца с периодом 365,25636 средних солнечных суток. Этот период называется сидерическим или звёздным годом.
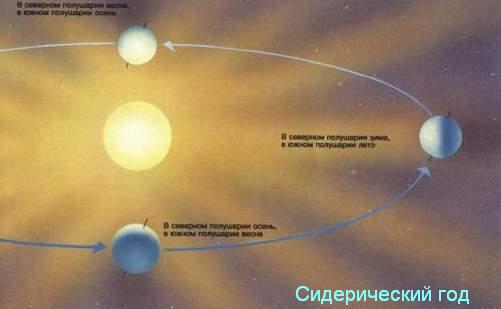

А ещё астрономы знают тропический год, драконический год…. Это тоже в некотором смысле периоды обращения Земли вокруг Солнца.
Итак, какой год взять за основу солнечных календарей?
4. Что такое тропический год?
Земля обращается вокруг Солнца.
А земному наблюдателю представляется, что Солнце перемещается по небу среди звёзд; так думали в древности, в античные времена и в средневековье.
В июне-июле Солнце далеко смещается в северное полушарие неба, — в то полушарие неба, где расположена Полярная звезда. Поэтому Солнце сильно прогревает северное полушарие Земли, где в это время — лето. Наоборот, в декабре-январе Солнце далеко уходит в южное полушарие неба, поэтому оно прогревает южное полушарие Земли, и лето там, а в северном полушарии Земли в декабре-январе зима.
Это наглядно видно на карте экваториальной области неба:
Здесь фиолетовая линия — небесный экватор. Выше него — прилегающая к экватору часть северного полушария неба, ниже — экваториальная часть южного полушария.
Красная линия изображает годовой путь Солнца по небу, называемый эклиптикой. Изображение Солнца на карте перемещается вдоль эклиптики справа налево.
Дважды в год, в дни весеннего (20-21 марта) и осеннего равноденствий (23 сентября), Солнце бывает на небесном экваторе в точках весеннего и осеннего равноденствия. Наверху подписаны сезоны года для северного полушария Земли, когда Солнце находится в соответствующей области неба.
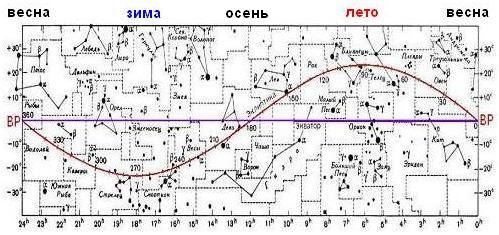

Солнце, проходя через точку весеннего равноденствия, — на карте она обозначена буквами ВР, — попадает из южного полушария неба в северное. Именно момент прохождения Солнца через точку весеннего равноденствия является началом астрономической весны. По своей сути этот момент является переходным от зимы к лету для северного полушария Земли.
Ну, сами посудите, как же может быть иначе? Летом дни длинные, зато ночи короткие, а зимой всё наоборот. В день весеннего равноденствия продолжительности дня и ночи в точности уравниваются1. Поэтому момент прохождения Солнца через точку весеннего равноденствия и принят за начало астрономической весны.
Промежуток времени между двумя последовательными прохождениями Солнца через точку весеннего равноденствия называется тропическим годом. Т.е. была весна (в северном полушарии Земли), а потом снова наступит весна.
Это значит, что сезоны года повторяются с периодом, равным тропическому году.
По современным данным его продолжительность на 1 января 2000 года равна 365,2421897 ср. солн. суток или 365 дней 5 часов 48 минут 45,19 секунды.
5. Почему у разных годов разная продолжительность?
Итак, продолжительность
— звёздного (сидерического) года 365, 25636 ср. солн. суток,
— аномалистического года 365,2596 ср. солн. суток,
— тропического года 365,2422 ср. солн. суток
С точки зрения геометрии и кинематики именно звёздный год и есть тот самый период, с которым Земля обращается вокруг Солнца.
Орбита, по которой Земля обращается вокруг Солнца, под воздействием планет солнечной системы, особенно таких, как Юпитер и Сатурн, со временем немного меняется. В частности перигелий орбиты Земли очень медленно движется так, что Земле приходится его догонять, а на это требуется время. Поэтому аномалистический год длиннее звёздного.
Тропический год, наоборот, короче звёздного, потому что точка весеннего равноденствия сама медленно движется по небу навстречу Солнцу, следовательно, Солнце и точка весеннего равноденствия встречаются раньше, чем Земля сделает полный оборот вокруг Солнца.
Т.е. равноденствия наступают немного раньше, «чем положено». Такое явление, получившее название «предварение равноденствий», объясняется прецессией земной оси. Оно было открыто основоположником научной астрономии Гиппархом из Никеи около 120 года до н.э. , а также независимо от него китайским астрономом Юй Си около 330 г. нашей эры.
Какой год самый главный? — Правильный ответ вы, наверное, уже и сами знаете.
— В небесной механике естественным образом возникает и поэтому является самым главным аномалистический год.
— Если нужно охарактеризовать обращение Земли вокруг Солнца в пространстве, — то главным является звёздный год.
— В теории солнечных календарей главным является тропический год, потому что сезоны года повторяются с периодом, равным тропическому году.
— Наконец, предсказания солнечных и лунных затмений выполняются на основе т. н. драконического года (346,620 ср. солн. суток).
6. Как измерить продолжительность тропического года?
Древний человек, у которого нет никаких астрономических инструментов, мог бы поступить так. В южной стене прочного помещения или пещеры делается такое отверстие, в которое прямые солнечные лучи в полдень попадают только дважды в год, — весной и осенью, а затем подсчитывается количество прошедших суток и лет.
Количество суток определяется по чередованию дня и ночи. Счёт лет следует начинать от дня появления весеннего солнечного луча, а затем наблюдать следующие появления. При этом нужно иметь в виду, что в какие-то годы наблюдения могут не получиться из-за плохой погоды.
В результате таких примитивных наблюдений станет известно, m суток составляют n лет. Тогда средняя продолжительность тропического года будет приближённо равна дроби m/n.
Спустя 20 лет можно будет утверждать, что продолжительность тропического года приблизительно равна 365,25 суток, что достаточно для создания юлианского календаря. Для создания календаря, подобного григорианскому, придётся наблюдать несколько сотен лет.
И ещё. Для определения продолжительности тропического года можно также наблюдать полуденную высоту Солнца, которая, как известно, минимальна в дни солнцестояний. Известно, что знаменитый древнегреческий астроном Метон для наблюдения солнцестояний воздвигал свои стелы (колонны) и инструменты в Афинах у самой площади народных собраний.
Около 125 до н.э. Гиппарх из Никеи уточнил продолжительность тропического года и синодического месяца, — промежутка времени между двумя последовательными, одинаковыми фазами Луны.
Согласно Гиппарху 304 солнечных года соответствуют 3760 лунным месяцам. Это позволило ему получить более точные значения продолжительности и тропического года, и синодического месяца, приблизив их к истинным значениям.
По данным Гиппарха солнечный год равнялся 365 дням 5ч 55 мин 16 сек, а лунный месяц — 29 дням 12 ч 44 мин 2,5 сек. Первая из этих величин всего лишь на 6 мин 30,41 сек больше принятого в настоящее время значения, а вторая — на 0,5 сек меньше.
Современное значение для продолжительности тропического года таково: на 1 января 2000 года он равен 365,2421897 ср. солн. суток или 365 дней 5 часов 48 минут 45,19 секунды.
7. В чём главная проблема солнечных календарей.
Календарный год должен содержать целое число суток, — альтернативная возможность даже не обсуждается, потому что иначе будет очень неудобно измерять время.
Тропический год длиннее, чем 365 суток на 0,2422 суток. Поэтому, если принять продолжительность календарного года в 365 суток, то новый год будет наступать раньше, чем положено, на 0,2422 суток. За четыре года ошибка достигнет примерно одних суток, за 120 лет она будет равна целому месяцу, а за 360 лет — целому сезону! Это значит, что когда календарь указывает на Новый год, на самом деле ещё осень.
Отсюда понятно: чтобы между сезонами года и календарём не было расхождений, необходимо точное равенство календарного и тропического года.
Итак, календарный год должен содержать целое число суток. Тропический год не содержит целое число суток. Поэтому они не могут быть в точности равны.
Противоречие.
В прошлом сообщении отмечено противоречие: чтобы календарь был точный, нужно добиться строгого равенства календарного и тропического года, — что невозможно. Потому что календарный год должен содержать целое число средних солнечных суток, а продолжительность тропического года равна 365,2422 средних солнечных суток.
Противоречие разрешается введением високосных годов.
Допускается, что разные календарные года могут содержать разное число целых суток. При этом требуется, чтобы средняя продолжительность календарного года была в точности равна тропическому году.
Принимается, что обычный год содержит 365 суток, а високосный год — 366 суток.
Это наиболее простое и разумное решение.
Конечно, можно иметь не два, а три, четыре, пять и т.д., видов годов разной продолжительности. Или, например, простой год может иметь 363 суток, а високосный 370 суток. — Но такие усложнения совершенно ни к чему, потому что они не дают ни малейшей выгоды в смысле упрощения календарной системы.
8. Арифметическая теория солнечных календарей.
Посмотрим, как накапливается расхождение между показаниями самого простого календаря, — древнеегипетского, все годы которого имеют одинаковую продолжительность 365 ср. солн. суток и сезонами года, которые повторяются с периодом в 365, 2422 ср. солн. суток.
| Прошедшее время в годах | Ошибка древнеегипетского календаря в средних солнечных сутках | Поправка, которую нужно прибавить или отнять, чтобы получить ближайшее целое число суток |
| 1 | 0,2422 | 0,2422 |
| 2 | 0,4844 | 0,4844 |
| 3 | 0,7266 | 0,2734 |
| 4 | 0,9688 | 0, 0312 |
| 5 | 1,2110 | 0,2110 |
| 6 | 1,4532 | 0,4532 |
Обращаю ваше внимание на третью колонку таблицы. Числа в ней является поправкой, которая показывают, насколько накопившаяся ошибка отличается от ближайшего целого числа суток.
Неустранимой является лишь та часть ошибки (см. вторую колонку), которая содержит дробное число суток. Наоборот, ту часть ошибки, которая является целым числом суток, можно легко устранить введением високосных годов.
Поэтому, именно поправка является мерой точности календаря, — чем меньше поправка, тем более точен календарь.
Из таблицы следует, что возможен солнечный календарь, называемый юлианским календарём, с периодом в четыре года, среди которых три простых и один високосный год.
Юлианский календарь элементарный, но, как оказалось, довольно точный. Ниже будет показано, что ошибка юлианского календаря составляет 1 сутки за 128 лет.
И на этом можно остановиться. — В самом деле, если кто и проживёт 128 лет, то ошибку в 1 сутки уж точно не заметит!
Но, как говорится, нет предела совершенству…
Поэтому продолжаем таблицу:
| Прошедшее время, в годах, т.е. число лет в календарном периоде, n | Ошибка древнеегипетского календаря в средних солнечных сутках | Поправка, которую нужно прибавить или отнять, чтобы получить целое число суток | Число високосных лет в периоде, m |
| 4 | 0,9688 | 0, 0312 | 1 |
| 5 | 1,2110 | 0,2110 | 1 |
| . . . | . . . | . . . | |
| 28 | 6,7816 | 0,2184 | 7 |
| 29 | 7,0238 | 0,0238 | 7 |
| 30 | 7,2660 | 0,2660 | 7 |
| 31 | 7,5082 | 0,4918 | 8 |
| 32 | 7,7504 | 0,2496 | 8 |
| 33 | 7,9926 | 0,0074 | 8 |
Здесь опущены многие результаты, которые хуже, т.е. менее точны, чем юлианский, четырёхлетний период, а точные календарные системы помечены красным цветом.
Продолжаем эту таблицу, но теперь опускаем все результаты, которые менее точны, чем те, которые уже имеются.
| Прошедшее время, в годах, т.е. число лет в календарном периоде, n | Ошибка древнеегипетского календаря в средних солнечных сутках | Поправка, которую нужно прибавить или отнять, чтобы получить целое число суток | Число високосных лет в периоде, m |
| 4 | 0,9688 | 0, 0312 | 1 |
| 29 | 7,0238 | 0,0238 | 7 |
| 33 | 7,9926 | 0,0074 | 8 |
| 128 | 31,0016 | 0,0016 | 31 |
| 545 | 131,9990 | 0,0010 | 132 |
Оказывается, в точности такую же таблицу можно легко получить с помощью цепных (непрерывных) дробей. Но поскольку теперь в школах непрерывные дроби не изучаются и, следовательно, многие люди слышат об них впервые, пришлось обойтись без таких дробей.
Ниже приводится сводная таблица наиболее известных солнечных календарей в порядке возрастания их точности.
| Название календаря | Длительность календарного периода в годах, n | Число простых лет в периоде, n – m | Число високосных лет в периоде, m | Среднегодовая ошибка календаря (сутки/год), Δ | Период (в годах), за который накопится ошибка в одни сутки. |
| Древнеегипетский | 4 | 4 | 0 | – 0,2422 | 4 |
| Юлианский | 4 | 3 | 1 | +0,00780 | 128 |
| 29-летний | 29 | 22 | 7 | –0,00082 | 1220 |
| Григорианский | 400 | 303 | 97 | +0,00030 | 3280 |
| Омара Хайяма | 33 | 25 | 8 | +0,00022 | 4500 |
| Новоюлианский | 900 | 682 | 218 | +0,00002 | 50.000 |
| Иоганна Медлера | 128 | 97 | 31 | +0,00001 | 100.000 |
| 545-летний | 545 | 413 | 132 | +0,00000 | Более 100.000 |
Число средних солнечных суток в календарном периоде, состоящем из n лет равно: [365(n – m) + 366m], а n тропических лет длятся 365,2422n средних солнечных суток. Эти два числа не равны, так как календарная система обладает некоторой погрешностью.
Разность между этими двумя числами — ошибка календаря, которая накапливается за один календарный период. Разделив это число на n, получим среднегодовую ошибку календарной системы (пятый столбец последней таблицы):
Δ = [365(n – m) + 366m – 365,2422n]/n =
[365(n – m) + 366m]/n – 365,2422 = (m/n) – 0,2422.
Следовательно, целые сутки накопятся за (1/|Δ|) лет.
Например, для юлианского календаря: (m/n)=1/4=0,25.
Поэтому Δ = 0,25 – 0,2422 = 0,0078(сут/год). Сутки накапливаются за 1: 0,0078=128 лет.
При этом отметим, что такие большие значения, как 50.000 лет, 100.000 лет, до некоторой степени условны. Они вычислены в предположении, что продолжительность тропического года неизменна и равна в точности 365,2422 средних солнечных суток.
Но это не так. Продолжительность тропического года медленно меняется хотя бы потому, что вращение Земли постепенно тормозится из-за приливов, и, кроме того, орбита Земли меняется вследствие планетных возмущений.
Да и кому нужны здесь точные цифры? Например, ошибка, равная одним суткам, в новоюлианском календаре накапливается или за 43.500 лет, или за 50.000 лет, — не всё ли равно?! Пусть тот, кому нужна точность, доживёт и проверит!
9. О правилах високосных годов
Представим себе, что в григорианском календаре, сначала пройдут подряд все 97 високосных лет, а потом 303 простых года. Такой календарь будет, как мы знаем, давать ошибку на протяжении календарного периода одни сутки за Δ=3280 лет.
Но жить с таким календарём не лучше, чем с древнеегипетским! В самом деле, за 97 лет должно быть примерно 24 високосных года. Поэтому окажется 97–24=73 високосных года лишних, откуда следует, что ошибка такого календаря будет достигать δ=73 суток, — более двух месяцев.
Такую ошибку все заметят!
После чего ошибка постепенно уменьшится почти до нуля, потому что все оставшиеся 303 года будут простыми.
Этот пример показывает, что
— нужно различать среднегодовую ошибку (Δ) и текущую ошибку календаря (δ).
— важно сформулировать хорошие правила високосных годов, т.е. такие правила, которые удачно распределяют високосные годы внутри календарного периода.
Выведем формулу, которая позволит проводить диагностику правил високосных годов, — какие правила лучше, а какие хуже.
Допустим, что прошло t лет (t ≤ n), из которых, согласно правилу високосных годов, было b високосных и t-b простых. Тогда текущая ошибка календаря будет равна:
δ = |366b + 365(t — b) – 365,2422t| =
= |b – 0,2422t|.
Пример.
Правило високосных годов юлианского календаря:
Если порядковый номер года делится без остатка на 4, то год високосный, если нет, — то простой.
Рассмотрим текущую ошибку юлианского календаря, начиная с 2011 года:
| t | № года | Какой год | b | δ |
| 1 | 2011 | простой | 0 | 0,2422 |
| 2 | 2012 | високосный | 1 | 0,5156 |
| 3 | 2013 | простой | 1 | 0,2734 |
| 4 | 2014 | простой | 1 | 0,0312 |
Таблица для 2012 года:
| t | № года | Какой год | b | δ |
| 1 | 2012 | високосный | 1 | 0,7578 |
| 2 | 2013 | простой | 1 | 0,5156 |
| 3 | 2014 | простой | 1 | 0,2734 |
| 4 | 2015 | простой | 1 | 0,0312 |
Ещё две таблицы для 2013 и 2014 года не приводятся, так как они не содержат текущую ошибку больше, чем 0,7578.
Отсюда понятно, максимальная текущая ошибка юлианского календаря составляет 0,7578 средних солнечных суток.
Точно также, перебрав всевозможные варианты, можно найти максимальную текущую ошибку для любой календарной системы с любым конкретным правилом високосных годов. Именно максимальная текущая ошибка является показателем качества правила високосных годов.
Однако на практике, оказывается, всё очень просто. — Високосные годы следует распределять в календарном периоде как можно более равномерно. Тогда ошибка не превысит 1,5 — 2 суток. Такую ошибку никто не заметит, кроме нескольких астрономов, но им — всё равно.
10. Взаимосвязь систем солнечных календарей.
Оказывается, что все солнечные календари, за исключением древнеегипетского и республиканского, являются производными от двух календарей, — юлианского и календаря Омара Хайяма.
Теперь пара слов на языке математики, а потом то же самое скажу простым человеческим языком.
Любую календарную систему с високосными годами можно изобразить матрицей–столбцом, где верхнее число, — количество високосных лет (m), среднее число — количество простых лет (n – m), нижнее число — календарный период (n).
Пусть МЮ и МОХ — матрицы, характеризующие юлианский календарь и календарь Омара Хайяма соответственно. Тогда матрица М любого солнечного календаря с високосными годами может быть представлена как линейная комбинация:
М = α МЮ + β МОХ ,
здесь α и β — некоторые целые числа.
| Название календаря | Длительность календарного периода в годах, n | Число простых лет в периоде, n – m | Число високосных лет в периоде, m | α | β |
| Древнеегипетский | 4 | 4 | 0 | — | — |
| Юлианский | 4 | 3 | 1 | 1 | 0 |
| 29-летний | 29 | 22 | 7 | – 1 | 1 |
| Григорианский | 400 | 303 | 97 | 1 | 12 |
| Омара Хайяма | 33 | 25 | 8 | 0 | 1 |
| Новоюлианский | 900 | 682 | 218 | – 6 | 28 |
| Иоганна Медлера | 128 | 97 | 31 | – 1 | 4 |
| 545-летний | 545 | 413 | 132 | – 4 | 17 |
На простом человеческом языке это означает, что если α, взятое из таблицы, умножить на 1, т.е. число високосных лет в юлианском календаре, а β, взятое из той же строки таблицы, умножить на 8, число високосных лет в календаре Омара Хайяма, то получим число високосных лет в соответствующем календаре. Аналогично для простых лет, а также для календарных периодов.
Например, для григорианского календаря, α=1, β=12:
Число високосных лет: 1х1+12х8=97;
Число простых лет: 1х3+12х25=303
Календарный период в годах: 1х4+12х33=400.
Это значит, что григорианский календарь составлен из 12 календарных периодов календаря Омара Хайяма, к которым добавлен один период юлианского календаря.
Ещё пример, для календаря Иоганна Медлера, α=–1, β=4:
Число високосных лет: (–1)х1+4х8=31;
Число простых лет: (–1)х3+4х25=97;
Календарный период в годах: (–1)х4+4х33=128.
Это значит, что календарь Иоганна Медлера составлен из четырёх календарных периодов календаря Омара Хайяма, а затем из них исключён один период юлианского календаря.
Впрочем, и без этого календарь Иоганна Медлера возникает очень естественно: в юлианском календаре ошибка в одни сутки набегает в течение 128 лет, и за это же время должно быть 128:4=32 високосных года. В календаре Иоганна Медлера только 31 високосный год, т.е. календарь Медлера получается в результате очевидного исправления юлианского календаря.
11. Три типа солнечных календарей.
Первый тип, когда ошибка не исправляется. Таков древнеегипетский календарь, где календарный год содержит 365 средних солнечных суток. Поэтому ошибка, возникающая вследствие того, что тропический год не укладывается в целое число средних солнечных суток, никак не исправляется.
Второй тип, когда ошибка исправляется нерегулярно, по мере необходимости. Таков республиканский календарь или, иначе, календарь французской революции (конец XVIII века — начало XIX века). В этом календаре ошибка совсем не накапливается, потому что компенсируется по мере необходимости, исходя из астрономических вычислений. Год в этом календаре начинался в полночь того дня, на который по среднему солнечному парижскому времени приходился момент осеннего равноденствия.
Високосные годы вследствие этого наступают то через четыре, то через пять лет. А точнее, семь раз подряд високосные годы повторяются через четыре года, а восьмой високосный год наступает через пять лет. Иначе говоря, в 33-летнем периоде високосными годами являются 4-й, 8-й, 12-й, 16-й, 20-й, 24-й, 28-й, и, наконец, 33-й.
Точно также високосные годы чередуются в календаре Омара Хайяма, при условии, что високосные годы расположены внутри 33-х летнего периода оптимальным образом. И это совсем неудивительно, — календарь Омара Хайяма является самым точным из простейших календарей.
Третий тип, промежуточный, когда ошибка исправляется введением високосных лет. Арифметическая теория таких календарей нами уже полностью рассмотрена. Оказалось, что все календари третьего типа являются производными от двух календарных систем, — юлианского календаря и календаря Омара Хайяма.
Всё!
Больше ничего в теории солнечных календарей от астрономии нет. Всё остальное в солнечных календарях — никак не детерминировано той или иной астрономической реальностью; некоторые особенности календарей, может быть, и были когда-то, в далёком прошлом, связаны с астрономическими явлениями, но теперь такая связь утрачена.
Список литературы
Для подготовки данной работы были использованы материалы с сайта https://vestishki.ru/
Дата добавления: 29.08.2013
Отрывок, характеризующий Солнечные сутки
К Кутузову накануне прибыл член гофкригсрата из Вены, с предложениями и требованиями итти как можно скорее на соединение с армией эрцгерцога Фердинанда и Мака, и Кутузов, не считая выгодным это соединение, в числе прочих доказательств в пользу своего мнения намеревался показать австрийскому генералу то печальное положение, в котором приходили войска из России. С этою целью он и хотел выехать навстречу полку, так что, чем хуже было бы положение полка, тем приятнее было бы это главнокомандующему. Хотя адъютант и не знал этих подробностей, однако он передал полковому командиру непременное требование главнокомандующего, чтобы люди были в шинелях и чехлах, и что в противном случае главнокомандующий будет недоволен. Выслушав эти слова, полковой командир опустил голову, молча вздернул плечами и сангвиническим жестом развел руки. – Наделали дела! – проговорил он. – Вот я вам говорил же, Михайло Митрич, что на походе, так в шинелях, – обратился он с упреком к батальонному командиру. – Ах, мой Бог! – прибавил он и решительно выступил вперед. – Господа ротные командиры! – крикнул он голосом, привычным к команде. – Фельдфебелей!… Скоро ли пожалуют? – обратился он к приехавшему адъютанту с выражением почтительной учтивости, видимо относившейся к лицу, про которое он говорил. – Через час, я думаю. – Успеем переодеть? – Не знаю, генерал… Полковой командир, сам подойдя к рядам, распорядился переодеванием опять в шинели. Ротные командиры разбежались по ротам, фельдфебели засуетились (шинели были не совсем исправны) и в то же мгновение заколыхались, растянулись и говором загудели прежде правильные, молчаливые четвероугольники. Со всех сторон отбегали и подбегали солдаты, подкидывали сзади плечом, через голову перетаскивали ранцы, снимали шинели и, высоко поднимая руки, натягивали их в рукава. Через полчаса всё опять пришло в прежний порядок, только четвероугольники сделались серыми из черных. Полковой командир, опять подрагивающею походкой, вышел вперед полка и издалека оглядел его. – Это что еще? Это что! – прокричал он, останавливаясь. – Командира 3 й роты!.. – Командир 3 й роты к генералу! командира к генералу, 3 й роты к командиру!… – послышались голоса по рядам, и адъютант побежал отыскивать замешкавшегося офицера. Когда звуки усердных голосов, перевирая, крича уже «генерала в 3 ю роту», дошли по назначению, требуемый офицер показался из за роты и, хотя человек уже пожилой и не имевший привычки бегать, неловко цепляясь носками, рысью направился к генералу. Лицо капитана выражало беспокойство школьника, которому велят сказать невыученный им урок. На красном (очевидно от невоздержания) носу выступали пятна, и рот не находил положения. Полковой командир с ног до головы осматривал капитана, в то время как он запыхавшись подходил, по мере приближения сдерживая шаг. – Вы скоро людей в сарафаны нарядите! Это что? – крикнул полковой командир, выдвигая нижнюю челюсть и указывая в рядах 3 й роты на солдата в шинели цвета фабричного сукна, отличавшегося от других шинелей. – Сами где находились? Ожидается главнокомандующий, а вы отходите от своего места? А?… Я вас научу, как на смотр людей в казакины одевать!… А?… Ротный командир, не спуская глаз с начальника, всё больше и больше прижимал свои два пальца к козырьку, как будто в одном этом прижимании он видел теперь свое спасенье. – Ну, что ж вы молчите? Кто у вас там в венгерца наряжен? – строго шутил полковой командир. – Ваше превосходительство… – Ну что «ваше превосходительство»? Ваше превосходительство! Ваше превосходительство! А что ваше превосходительство – никому неизвестно. – Ваше превосходительство, это Долохов, разжалованный… – сказал тихо капитан. – Что он в фельдмаршалы, что ли, разжалован или в солдаты? А солдат, так должен быть одет, как все, по форме. – Ваше превосходительство, вы сами разрешили ему походом. – Разрешил? Разрешил? Вот вы всегда так, молодые люди, – сказал полковой командир, остывая несколько. – Разрешил? Вам что нибудь скажешь, а вы и… – Полковой командир помолчал. – Вам что нибудь скажешь, а вы и… – Что? – сказал он, снова раздражаясь. – Извольте одеть людей прилично… И полковой командир, оглядываясь на адъютанта, своею вздрагивающею походкой направился к полку. Видно было, что его раздражение ему самому понравилось, и что он, пройдясь по полку, хотел найти еще предлог своему гневу. Оборвав одного офицера за невычищенный знак, другого за неправильность ряда, он подошел к 3 й роте. – Кааак стоишь? Где нога? Нога где? – закричал полковой командир с выражением страдания в голосе, еще человек за пять не доходя до Долохова, одетого в синеватую шинель. Долохов медленно выпрямил согнутую ногу и прямо, своим светлым и наглым взглядом, посмотрел в лицо генерала. – Зачем синяя шинель? Долой… Фельдфебель! Переодеть его… дря… – Он не успел договорить. – Генерал, я обязан исполнять приказания, но не обязан переносить… – поспешно сказал Долохов. – Во фронте не разговаривать!… Не разговаривать, не разговаривать!… – Не обязан переносить оскорбления, – громко, звучно договорил Долохов. Глаза генерала и солдата встретились. Генерал замолчал, сердито оттягивая книзу тугой шарф. – Извольте переодеться, прошу вас, – сказал он, отходя. – Едет! – закричал в это время махальный. Полковой командир, покраснел, подбежал к лошади, дрожащими руками взялся за стремя, перекинул тело, оправился, вынул шпагу и с счастливым, решительным лицом, набок раскрыв рот, приготовился крикнуть. Полк встрепенулся, как оправляющаяся птица, и замер. – Смир р р р на! – закричал полковой командир потрясающим душу голосом, радостным для себя, строгим в отношении к полку и приветливым в отношении к подъезжающему начальнику. По широкой, обсаженной деревьями, большой, бесшоссейной дороге, слегка погромыхивая рессорами, шибкою рысью ехала высокая голубая венская коляска цугом. За коляской скакали свита и конвой кроатов. Подле Кутузова сидел австрийский генерал в странном, среди черных русских, белом мундире. Коляска остановилась у полка. Кутузов и австрийский генерал о чем то тихо говорили, и Кутузов слегка улыбнулся, в то время как, тяжело ступая, он опускал ногу с подножки, точно как будто и не было этих 2 000 людей, которые не дыша смотрели на него и на полкового командира. Раздался крик команды, опять полк звеня дрогнул, сделав на караул. В мертвой тишине послышался слабый голос главнокомандующего. Полк рявкнул: «Здравья желаем, ваше го го го го ство!» И опять всё замерло. Сначала Кутузов стоял на одном месте, пока полк двигался; потом Кутузов рядом с белым генералом, пешком, сопутствуемый свитою, стал ходить по рядам. По тому, как полковой командир салютовал главнокомандующему, впиваясь в него глазами, вытягиваясь и подбираясь, как наклоненный вперед ходил за генералами по рядам, едва удерживая подрагивающее движение, как подскакивал при каждом слове и движении главнокомандующего, – видно было, что он исполнял свои обязанности подчиненного еще с большим наслаждением, чем обязанности начальника. Полк, благодаря строгости и старательности полкового командира, был в прекрасном состоянии сравнительно с другими, приходившими в то же время к Браунау. Отсталых и больных было только 217 человек. И всё было исправно, кроме обуви.