Созвездие Возничий относится к зимним, и лучше всего его наблюдать в декабре-январе, хотя уже с осени оно видно на востоке. По площади оно занимает 21 место среди всех 88 созвездий, поэтому в нем найдутся любопытные объекты для наблюдений, хотя и не такие эффектные, как, например, в Орионе или Тельце.
Название созвездия дано в честь мифического Эрихтония, который первым придумал двухколесную колесницу и за изобретательность помещенного Зевсом на небо. Это изобретение, кстати, помогло ему победить в войне и стать царем Афин.
Созвездие Возничий на небе
Созвездие Возничий располагается выше созвездий Орион и Близнецы, левее Тельца с ярким Альдебараном. Узнать его легко благодаря расположению звезд в виде пятиугольника, в верхнем углу которого ярко сияет Капелла – ярчайшая звезда созвездия и одна из самых ярких вообще на небе, в 0.1m.

Созвездие Возничий на небе.
В созвездии Возничего есть некоторые любопытные звезды и несколько объектов каталога Мессье, которые доступны для наблюдений и начинающими любителями астрономии.
Рычаговый коэффициент бета = безрычаговый коэффициент бета х х [1 + (1 — налоговая ставка) (долг/собственный капитал)]. [c.256] Коэффициент бета за период 1996-2000 гг. отражает этот средний левередж (рычаг). Для оценки безрычагового коэффициента бета (без долга) за период используется предельная налоговая ставка [c.255]
Безрычаговый коэффициент бета = [c.255]
Учет различий. В сущности, используя коэффициенты бета сопоставимых фирм, мы предполагаем, что все фирмы, которые занимаются данным видом деятельности, в одинаковой мере подвержены риску, связанному с данным видом деятельности, и имеют одинаковый операционный рычаг. Заметим, что процесс обременения и разгрузки коэффициентов бета с точки зрения долга позволяет нам учитывать различия в финансовом рычаге. Если наблюдаются значительные различия в операционном рычаге — скажем, в силу различий в структуре издержек, — то они также могут быть учтены. Для этого потребуется оценить коэффициент бета для вида деятельности, где воздействия операционного рычага получаются на основе безрычагового коэффициента бета [c.260]
В дополнение к коэффициентам бета для каждой фирмы, таблица содержит рыночный коэффициент долг/собственный капитал , эффективную налоговую ставку и уровень операционного рычага, полученный делением общих, сбытовых и административных расходов (которые мы рассматриваем как фиксированные) на другие операционные расходы (которые мы рассматриваем как переменные). Мы можем оценивать безрычаговый коэффициент бета для данного вида деятельности, используя средние этих величин [c.261]
Используя среднюю налоговую ставку в размере 25,95%, мы можем оценить безрычаговый коэффициент бета. [c.261]
Безрычаговый коэффициент бета = 0,79 / [1 + (1 — 0,2595) 0,7504] = 0,5081. [c.261]
Коэффициент бета для вида деятельности = безрычаговый коэффициент бета / [c.262]
Каждая из этих областей имеет очень разные характеристики риска, и безрычаговый коэффициент бета для каждого вида деятельности оценивается через рассмотрение сопоставимых компаний в каждом виде бизнеса. В нижеследующей таблице представлены эти оценки [c.263]
Безрычаговый коэффициент бета для компаний, производящих цемент = = 0,99/П + (1-0,342)(0,2706)] = 0,84. [c.264]
Безрычаговый коэффициент бета для объединенной фирмы может быть вычислен как средневзвешенная величина двух безрычаговых коэффициентов бета, когда веса основываются на рыночных стоимостях двух фирм. [c.266]
Безрычаговый коэффициент бета комбинации фирм = = 0,88 (36 418/51 116) + 0,81(14 698/51 116) = 0,86. [c.266]
Коэффициент долг/собственный капитал в сочетании с новым безрычаговым коэффициентом бета для объединенной фирмы даст новый коэффициент бета [c.267]
Безрычаговый коэффициент бета для аэрокосмических фирм = 0,87. [c.271]
Ставка по казначейским облигациям составляет 6%, а безрычаговый коэффициент бета других телекоммуникационных фирм равен 0,80. [c.299]
Сначала мы оценим стоимость собственного капитала на основе восходящего коэффициента бета, равного 0,85 (оцененного на основе безрычагового коэффициента бета для фирм, специализирующихся на потребительской продукции, и коэффициента долг/ собственный капитал для P G), безрисковой ставки 5,4% и премии за риск 4%. [c.439]
Безрычаговый коэффициент бета можно использовать для получения стоимости собственного капитала без учета долга. [c.536]
Безрычаговый коэффициент бета = 1,17/[1 + (1 — 0,3)(0,79)] = 0,75. [c.538]
Начнем со стоимости собственного капитала. Мы доказывали, что коэффициент бета собственного капитала будет меняться при колебаниях долгового коэффициента. В действительности, мы оценили рычаговый коэффициент бета как функцию коэффициента рыночная стоимость долга фирмы/ собственный капитал , безрычагового коэффициента беты и предельной налоговой ставки фирмы [c.542]
Таким образом, если мы сможем оценить безрычаговый коэффициент бета фирмы, то сумеем использовать его для оценки рычагового коэффициента бета фирмы при любом долговом коэффициенте. Этот рычаговый коэффициент бета может затем использоваться для вычисления стоимости собственного капитала при любом долговом коэффициенте. [c.542]
Во-первых, для дисконтирования денежных потоков нужно скорректировать стоимость акций или капитала так же, как и размер наличности. Говоря конкретнее, необходимо использовать безрычаговый коэффициент бета, представляющий собой средневзвешенное значение безрычагового коэффициента бета по оборотным активам и безрычагового коэффициента бета по денежным средствам и ликвидным ценным бумагам. Например, подобный коэффициент бета сталелитейной компании, где наличность представляет 10% ценности, будет средневзвешенным значением безрычагового коэффициента бета сталелитейных компаний и такого же коэффициента по наличности (он обычно равен нулю). Если бы 10% инвестировались в рисковые ценные бумаги, то коэффициент бета надо бы было скорректировать. Это можно сделать, используя восходящие коэффициенты бета, однако обнаруживается, что это гораздо труднее сделать, если коэффициент бета получается на основе регрессии. [c.567]
Безрычаговый коэффициент бета, который можно получить из регрессионного коэффициента бета, отражает средние кассовые остатки (как процент от ценности фирмы) за период регрессии. Таким образом, если фирма поддерживает этот коэффициент на постоянном уровне, то вы оказываетесь в состоянии прийти к правильному безрычаговому коэффициенту бета. [c.567]
Существует и вторая область различий. При получении оценок коэффициентов бета для фирм из нефинансового сектора мы подчеркивали важность безрычаговых коэффициентов бета (при этом не важно, являются ли [c.774]
Безрычаговый коэффициент бета для компании Boeing за период 1996-2000 гг. равен 0,51. Коэффициент бета с учетом долгового бремени при различных уровнях задолженности может быть оценен следующим образом [c.255]
Этот коэффициент бета, полученный с учетом долга, основывается на неявном предположении о том, что все производители обуви имеют аналогичный операционный рычаг. Фактически, мы можем откорректировать безрычаговый коэффициент бета, принимая во внимание средний коэффициент постоянные издержки/переменные издержки для бизнеса, а затем устранить эффект операционного рычага для Vans Shoes [c.262]
Безрычаговый коэффициент бета Vans = 0,3576 (1 + 0,3116) = 0,4691, Рычаговый коэффициент = 0,4691 [1 + (1 — 0,3406) 0,0941] = 0,4981. [c.262]
В коммерческой авиации не существует фирм, которые можно было бы по-настоящему сравнивать. Мы рассматривали собственный коэффициент бета компании Boeing перед ее экспансией в сферу оборонного бизнеса и вычислили безрычаговый коэффициент бета (без учета долга), используя эту оценку. Для ISDS мы использовали 17 фирм, которые получали основной объем своей выручки от оборонных контрактов, и вычислили средний коэффициент бета и коэффициент долг/собственный капитал для этих фирм. Безрычаговые коэффициенты бета были вычислены с использованием этих средних. Ценность каждого подразделения оценивалась по выручке от каждого сегмента и стандартного коэффициента на ее основе для данного вида деятельности. Безрычаговый коэффициент бета для компании Boeing в 2000 г. можно оценить, если взять взвешенный на основе ценности средний коэффициент бета каждой из различных сфер бизнеса. Он отображен в столбце как величина 0,8774. [c.263]
Оценку коэффициента бета компании Titan ement мы начинаем с определения сопоставимых фирм (т. е. с поиска других греческих компаний, производящих цемент). Однако мы нашли только одну сопоставимую фирму. Если мы расширим наш список, чтобы включить туда цементные компании со всей Европы, то увеличим выборку до 9 фирм. Поскольку у нас нет причин ограничивать наше сравнение только европейскими фирмами, мы можем решить рассмотреть средний коэффициент бета для цементных компаний по всему миру. В эту выборку попадают 108 фирм со средним коэффициентом бета 0,99, средней налоговой ставкой 34,25% и средним коэффициентом долг/собственный капитал 27,6%. Мы использовали эти величины для получения безрычагового коэффициента бета, который оказался равным 0,84. [c.264]
Для оценки воздействия приобретения на коэффициент бета компании Boeing мы сначала изучим воздействие слияния на риск, связанный с данным видом деятельности, объединенной фирмы, — путем оценки безрычагового коэффициента бета (без учета долга) двух компаний и вычисления общего безрычагового коэффициента бета объединенной фирмы. [c.266]
Embraer — бразильская аэрокосмическая фирма. Для оценки стоимости ее собственного капитала мы сначала оценим безрычаговый коэффициент бета путем рассмотрения аэрокосмических фирм по всему миру. [c.271]
Вы анализируете Tiffany ompany, крупную компанию, занимающуюся розничными продажами, и находите, что регрессионная оценка коэффициента бета фирмы равна 0,75. Стандартная ошибка для оценки коэффициента бета составляет 0,50. Вы также замечаете, что средний безрычаговый коэффициент бета (без учета долга) сопоставимых фирм, работающих в той же области, равен 1,15. [c.299]
Компания hur h Dwight в 1993 г. имела коэффициент бета, равный 0,85, а безрычаговый коэффициент бета, предположительно, не будет изменяться со временем. [c.463]
Рычаговый Рычаговый коэффици- Безрычаговый коэф-коэффициент бета ент бета преобразуется в фициент бета преоб-безрычаговый коэффи- разуется в рычаговый циент бета через коэф- коэффициент бета фициент валовой долг/ через коэффициент рыночная стоимость соб- чистый долг/рыноч-ственного капитала . ная стоимость собственного капитала . [c.531]
Для оценки ценности фирмы без учета долга мы сначала вычислим безрычаговый коэффициент бета. Коэффициент бета компании Tube Investment равен 1,17. Теку- [c.537]
Стоимость собственного капитала компании Boeing при различных значениях долгового коэффициента можно вычислить, используя безрычаговый коэффициент бета фирмы, а также коэффициент долг/собственный капитал фирмы при каждом уровне долга. Мы используем рычаговые коэффициенты бета, применявшиеся при оценке стоимости собственного капитала. Первый шаг в этом процессе — это вычисление текущего безрычагового коэффициента бета фирмы исходя из текущего коэффициента рыночная стоимость долга/собственный капитал и налоговой ставки, равной 35%. [c.544]
Звезды созвездия Возничий
В этом созвездии есть любопытные звезды. Хотя внешне они выглядят, как и все прочие, все-таки полезно найти их на небе и взглянуть на них для общего развития.
Капелла – ярчайшая звезда в созвездии Возничего
Когда-то, примерно 210 — 160 тысяч лет назад, Капелла была самой яркой звездой на небе, хотя видеть это могли разве что динозавры. 240 000 лет назад эта звезда была от нас ближе всего – в 28 световых годах, но с тех пор расстояние сильно увеличилось.
Эта звезда сейчас удалена от нас на 42 световых года, и на самом деле она двойная. Правда, в телескоп это увидеть не получится, так как компоненты в этой системе расположены на расстоянии всего в 2/3 расстояния от Земли до Солнца – порядка 100 миллионов километров.
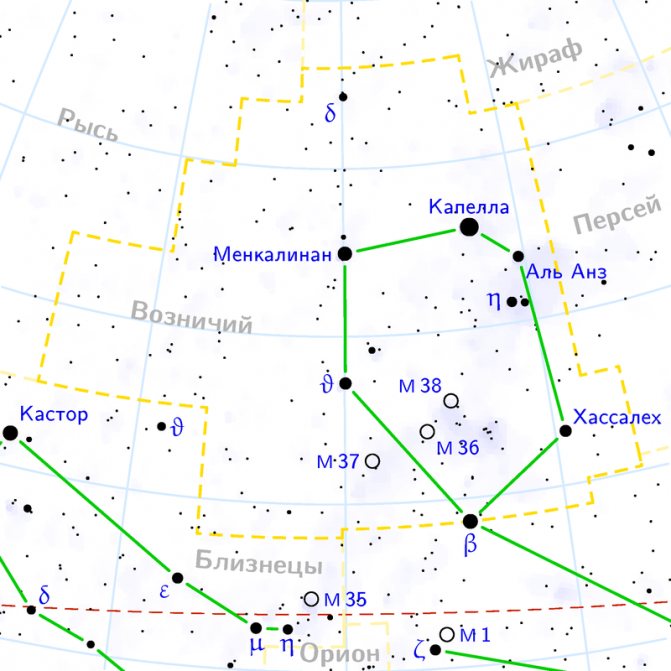

Карта созвездия Возничий.
Оба компонента в системе Капеллы – гиганты, один в 77 раз ярче Солнца, а другой – в 78 раз. Компонент A – красный гигант, который уже сжег свой водород и теперь выжигает гелий. Второй компонент B также находится на этом пути – водород уже кончился, но гелий еще в реакциях не используется. Обе звезды в 2.5 раза тяжелее Солнца и обращаются вокруг центра масс за 104 суток.
Когда эти два гиганта, расположенных довольно тесно, начнут расширяться, их оболочки могут соприкоснуться, хотя произойдет это еще не скоро.
На расстоянии в 1 световой год от пары гигантов расположена еще пара звезд – красных карликов, которые также связаны друг с другом довольно тесно. И эта пара также имеет с парой гигантов общий центр тяжести. Так что на самом деле Капелла – четырехкратная звезда, состоящая из пары красных гигантов и пары красных карликов.


Сравнительные размеры компонентов системы Капеллы и Солнца.
Бета Возничего – Менкалинан
Эта звезда имеет собственное имя Менкалинан, и представляет собой тройную звезду. В центре системы – пара субгигантов, каждый из которых в 48 раз ярче Солнца. Эти звезды истратили свой водород и начали увеличиваться. Расположены они очень тесно – всего в 0.08 а.е. друг от друга, что в 5 раз меньше расстояния от Солнца до Меркурия.


Бета Возничего — Менкалинан
Из-за такого близкого расположения взаимное приливное воздействие столь велико, что звезды имеют не сферическую, а овальную форму, и расположены друг к другу одной стороной. Когда они увеличатся, возможно, произойдет соприкосновение, как и в системе Капеллы.
Менкалинан расположен в пространстве таким образом, что каждые 3.96 суток происходит затмение одной звезды другой и общая яркость падает на 0.1m. Так что это затменно-переменная звезда.
На расстоянии в 330 а.е. от пары больших звезд вращается еще одна – красный карлик. Без телескопа его увидеть не получится.
Эпсилон Возничего – Алмааз
Звезда ε Возничего также имеет собственное имя – Алмааз. Эта звезда очень далеко, до нее примерно 2000 световых лет, и тот факт, что мы все-таки её видим даже невооруженным глазом, говорит о незаурядных свойствах.
Это затменно-переменная звезда, которая состоит из двух компонентов. Главный из них – яркий белый сверхгигант, который сам по себе пульсирует с периодом в 66 дней. Эта звезда в 100-200 раз больше Солнца и ярче его в 40-60 тысяч раз!
А вот второй компонент — весьма странный объект, природу которого долго не могли понять. Считалось даже, что это черная дыра или огромная полупрозрачная звезда.
Дело в том, что затмения, когда яркость Алмааза падает с 2.92m до 3.83m, случаются раз в 27 лет, и длятся 640-730 дней. Это значит, что второй компонент находится очень далеко от первого. Чтобы затмить сверхгигант с такого расстояния на такой длительный срок, он должен иметь невероятно большой размер.
Сейчас существует теория, что второй компонент в системе эпсилона Возничего – двойная система, окруженная пылевым диском. При прохождении этой большой туманности на фоне сверхгиганта и происходит падение его яркости, которое мы и наблюдаем раз в 27 лет.


Возможно, так выглядит второй компонент системы Эпсилон Возничего.
Эпсилон Возничего – звезда, которая вызывает пристальное внимание астрономов. Здесь не все так просто, как кажется. Природа второго компонента этой системы до сих пор остается невыясненой, так как его сложно наблюдать. Еще совсем недавно выдвигалось немало гипотез, но ни одна не нашла подтверждения. Теория насчет пылевого диска пока наиболее реальна, но тоже требует дополнительных исследований. Найдя эту звезду на небе, вспомните, что это один из самых загадочных объектов, хранящий немало секретов.
Дзета Возничего
Звезда ζ Возничего называется Хедус (в латинском варианте), или Садатони (в арабском). Это тоже впечатляющая звезда, а вернее – двойная система, которую мы видим как затменную переменную. Она удалена от нас очень далеко – на 784 световых года.
Главный компонент в этой системе – яркий оранжевый гигант, в 148 раз больше Солнца, почти в 6 раз массивнее, и в 4800 раз ярче. Вторая звезда – горячая бело-голубая, лишь в 4.8 раз массивнее Солнца и в 4.5 раз больше, однако и она в 1000 раз ярче нашего светила.
Период вращения этой пары – 2.66 года. В этой системе нет такой интриги, как у эпсилона Возничего, однако это весьма впечатляющая пара звезд. Эта система – жаркое место.
Начинается аномальное затмение звезды Эпсилон Возничего
Раз в 27 лет довольно яркая звезда ε (эпсилон) Возничего (ε Aurigae) тускнеет — начинается ее затмение каким-то объектом, обращающимся вокруг звезды с периодом в 27 лет и один месяц. Длится затмение почти два года — в течение полугода яркость Aurigae медленно снижается, пока не достигнет половины дозатменного уровня. Еще чуть меньше года звезда проводит в минимуме блеска, а затем полгода выбирается на обычный уровень, чтобы прожить на нем еще 25 лет.


Расписание затмения (приблизительное):
- Начало частной фазы — 6 августа 2009 года.
- Начало полной фазы — 21 декабря 2009 года.
- Середина затмения — 1 августа 2010 года.
- Конец полной фазы — 12 марта 2011 года.
- Конец частной фазы — 15 мая 2011 года.
Очередное затмение начинается как раз в эти дни, формальная дата — 6 августа. Тем не менее указывать эту дату с точностью до одного дня неверно. Это все равно что с точностью до 1 мм проводить на холмистой Валдайской возвышенности черту, от которой начинается спуск к Балтийскому морю: и в промежутках между затмениями эпсилон Возничего слегка меняет свой блеск, немного пульсируя.
Затменные переменные
Светила, с которыми регулярно случаются затмения, астрономам хорошо известны. Их так и называют — затменно-переменные звезды. Период этих изменений меняется от часов до десятилетий (ε Возничего как раз рекордсмен среди известных затменно-переменных), а глубина затмения — от почти 100−процентной до долей этого самого процента.
Глубина зависит от геометрии системы и размеров затмевающего звезду тела: крупный сосед может закрыть звезду целиком, а маленькая планета лишь чуть-чуть изменит блеск, когда проходит по диску светила. Зависит глубина и от того, как ярко светится затмевающее тело: его-то поверхность мы продолжаем видеть и во время затмения.
Затменно-переменные звезды сыграли ключевую роль в понимании физики звезд, их реального строения и эволюции. Изучение параметров затмения (глубины, продолжительности, периода) позволяет вычислить характеристики звезд, недоступные прямому измерению — размер, массу, параметры орбиты. Именно так долгие годы проверяют и уточняют теории звездного строения, а потому наблюдения затменно-переменных звезд продолжаются до сих пор.
Загадка из Возничего
Для ε Возничего все эти параметры также удалось определить. Ее масса, к примеру, составляет около 15 масс Солнца, а размер и температура очень хорошо соотносятся с наблюдаемой светимостью. Если верить анализу наблюдений, вокруг главного светила крутится звезда примерно такой же массы, и это именно она вызывает затмения.
Проблема лишь в том, что этой звезды почему-то не видно. И вызванные ею затмения тянутся необъяснимо долго — как будто размер темного объекта составляет 4 млрд км. В классических книжках по астрономии, изданных несколько десятилетий назад, вторую компоненту даже официально именовали «самой крупной из известных звезд». Согласно более или менее принятой сегодня модели, настоящая причина затмений — мощный газопылевой диск, окружающий вторую компоненту системы. Он поглощает ее свет, и он же удлиняет затмение видимой компоненты. Именно его медленное вползание на яркую звезду мы можем наблюдать в эти дни.
Быстрые перемены
Правда, на этом загадки не заканчиваются. Примерно в середине затмения ε Возничего иногда начинает лихорадочно менять блеск, как будто в закрывающем ее диске имеются какие-то окна. К тому же от затмения к затмению его продолжительность сокращается — и это притом что длительность полной фазы затмения за последние полвека увеличилась на четверть. Если экстраполировать прежние изменения на нынешний минимум, выход из него может составить всего несколько недель.
Как объяснить эти изменения, ученые пока не знают. Возможно, яркая центральная звезда заметно меняется в размерах, но тогда эти явления должны происходить на очень короткой временной шкале, совсем не характерной для звездной эволюции. Возможно, мы наблюдаем какие-то непонятные процессы в темном диске, которые постепенно меняют его геометрию.
Покажи козу теории
Устоит ли модель темного диска после нынешнего затмения, пока не может сказать никто. Чтобы проверить ее, профессиональным астрономам нужно как можно больше измерений блеска светила.
Помочь «свалить» теорию может любой желающий.
Найти ε Возничего на небе совсем несложно. Эта звездочка третьей (пока!) звездной величины находится всего в 3,5 градусах (семи лунных дисках) от яркой Капеллы. Переменная звезда — это вершина острого угла крохотного вытянутого треугольничка, примыкающего к Капелле. Именно с яркой звезды и стоит начинать поиски; в России, за исключением самого юга страны, она никогда не заходит за горизонт. Зимней ночью желтая Капелла украшает небо высоко над Орионом; летом ее можно найти невысоко в северной части неба.
Чтобы оценить блеск светила, стоит подобрать две звезды для сравнения — одну чуть ярче, другую чуть слабее, чем оцениваемая звезда, — и попробовать поместить последнюю на мысленной шкале между ними. Две других вершины маленького треугольника – левая η (эта) и правая ζ (дзета) Возничего очень хорошо подходят для этой цели. На данный момент обе они тусклее загадочной ε, но уже скоро картина изменится: в ближайшие недели переменная должна сравняться с этой, а через полгода ее блеск упадет примерно до уровня дзеты.
Если, конечно, эта звезда не преподнесет нам новых сюрпризов. Именно для того чтобы вовремя заметить их, астрономы и просят публику приглядеться к загадочной звезде. Ведь следующий шанс наступит лишь в 2036 году.
Звездные скопления в созвездии Возничего
В этом созвездии есть целых три рассеянных звездных скопления – М36, М37 и М38. Они расположены близко друг к другу и составляют практически тройное скопление. Самое яркое из них – М37.


Звездное скопление М37.
Расположены все три скопления примерно на одном расстоянии от нас – 4400 световых лет, хотя М38 немного ближе. Состоят они в основном из горячих белых звезд.
Все три скопления несложно наблюдать даже в небольшой любительский телескоп, а найти их можно и в бинокль.


Facebook
Бета Возничего
| Кратная звезда | |
| Менкалинан | |
| Система Бета Возничего в программе Celestia | |
| Наблюдательные данные (Эпоха J2000.0) | |
| Тип | Тройная звезда |
| Прямое восхождение | 05ч 59м 31,70с |
| Склонение | +44° 56′ 33,51″ |
| Расстояние | 82,1 св. года (25,2 ) |
| Видимая звёздная величина (V ) | V max = +1.89m, V min = +1.98m, P = 3,96 д |
| Созвездие | Возничий |
| Астрометрия | |
| Лучевая скорость (Rv ) | −18,2 км/c |
| Собственное движение | |
| • прямое восхождение | −56,41 mas в год |
| • склонение | −0,88 mas в год |
| Параллакс (π) | 39.72 ± 0.78 mas |
| Абсолютная звёздная величина (V) | V max = -0.11m, V min = -0.02m, P = 3.96 д |
| Спектральные характеристики | |
| Спектральный класс | A2IV+… C |
| Показатель цвета | |
| • B−V | +0.03 |
| • U−B | +0.05 |
| Переменность | |
| Физические характеристики | |
| Температура | 8954 К[1] |
| Металличность | 0[2] |
| Вращение | 40 км/с[3][4] |
| Часть от | Движущаяся группа звёзд Большой Медведицы |
| Коды в каталогах Менкалинан 34 Aurigae +44°1328, CCDM 05596+4457, FK5 227, 40183, HIP 28360, HR 2088, SAO 40750, ADS 4556, GC 7543, 3375 β Aur | |
| Информация в базах данных | |
| SIMBAD | данные |
| Звёздная система | |
| У звезды существует 3 компонента Их параметры представлены ниже: | |
| Шаблон:Компонент | |
| Шаблон:Компонент | |
| Шаблон:Компонент | |
| Информация в Викиданных ? | |
Бета Возничего
(β Aur/β Aurigae) — тройная звёздная система в созвездии Возничего. Имеет историческое название
Менкалинан
[5] от арабского منكب ذي العنان
манкаб зи’л-‘анан
[6] «плечо обладателя поводьев».[7].
Менкалинан
— звезда спектрального класса A с температурой поверхности 9200 К, похожая на Вегу или Сириус. Учитывая расстояния до него, которое равно 82 св. г. можно вычислить, что его яркость в 95 раз больше солнечной, что несколько больше, чем обычная яркость для такой звезды. Наблюдения показывают, что каждые 3.96 дня, в системе происходит частичное затмение и светимость звезды уменьшается, приблизительно, на одну десятую звёздной величины[8]. Таким образом, система состоит из двух почти идентичных звезд, каждая из которых, приблизительно, в 48 раз более яркая, чем Солнце и которые отдалённы друг от друга на расстояние, приблизительно, 0,08 а.е. (пятая часть расстояния между Солнцем и Меркурием). Обе звезды являются субгигантами, которые начали раздуваться и увеличивать яркость в результате истощения в ядре их основного топлива — водорода. Звезды настолько близки, что искажают форму друг друга приливными силами, период их вращения синхронизирован с периодом обращения и звёзды всегда повёрнуты друг к другу одной стороной.[9].
На расстоянии, по крайней мере, 330 а.е. вокруг пары звёзд вращается красный карлик невидимый невооруженным глазом. На таком расстоянии пара довольно больших звёзд, вряд ли может быть разрешена глазом и видна как одна звезда[9].
Менкалинан
возможно принадлежит к движущейся группе звёзд Большой Медведицы.