История открытия
Вкратце история его такова. Еще древние, наблюдая за движением планет на небе, догадались, что все они, вместе с Землей, «ходят» вокруг Солнца. Позднее, когда люди забыли то, о чем знали прежде, это открытие заново сделал Коперник. И тогда возник новый вопрос: как именно планеты ходят вокруг Солнца, каково их движение? Ходят ли они по кругу и Солнце находится в центре или они движутся по какой-нибудь другой кривой? Как быстро они движутся? И так далее.
Выяснилось это не так скоро. После Коперника снова настали смутные времена и разгорелись великие споры о том, ходят ли планеты вместе с Землей вокруг Солнца или Земля находится в центре Вселенной. Тогда человек по имени Тихо Браге (Тихо Браге (1546-1601) — датский астроном)
придумал, как можно ответить на этот вопрос. Он решил, что нужно очень внимательно следить за тем, где появляются на небе планеты, точно это записывать и тогда уже выбирать между двумя враждебными теориями. Это и было началом современной науки, ключом к правильному пониманию природы — наблюдать за предметом, записывать все подробности и надеяться, что полученные таким способом сведения послужат основой для того или иного теоретического истолкования. И вот Тихо Браге, человек богатый, владевший островом поблизости от Копенгагена, оборудовал свой остров большими бронзовыми кругами и специальными наблюдательными пунктами и записывал ночь за ночью положения планет. Лишь ценой такого тяжелого труда достается нам любое открытие.
Когда все эти данные были собраны, они попали в руки Кеплера (Иоганн Кеплер (1571-1630) -немецкий астроном и математик, был помощником Браге)
, который и пытался решить, как движутся планеты вокруг Солнца. Он искал решение методом проб и ошибок. Однажды ему показалось, что он уже получил ответ: он решил, что планеты движутся по кругу, но Солнце лежит не в центре. Потом Кеплер заметил, что одна из планет, кажется Марс, отклоняется от нужного положения на 8 угловых минут, и понял, что полученный им ответ неверен, так как Тихо Браге не мог допустить такую большую ошибку. Полагаясь на точность наблюдений, он решил пересмотреть свою теорию и в конце концов обнаружил три факта.
Третий закон
Квадрат единого времени по орбитальной линии пропорционален кубическому параметру усреднённого расстояния от самой планеты до Солнца. Данная теория имеет ещё одно название, постулат часто именуют законом гармонии. В этом случае происходит сравнение орбитального отрезка времени с радиусом планетной орбиты. Таким образом, для каждой планеты соотношение квадратных показателей периодов движения и среднего расстояния, возведённого в куб, до светила аналогично.
Немецкий учёный Иоганн Кеплер был тем, кто открыл законы движения планет вокруг Солнца. Данные постулаты способствовали установлению формы орбитальных путей, позволяли рассчитать период обращения и скорость, а также наблюдать изменение показателей скорости на участках сближения и отдаления от Солнца. Учёный доказал, что Земля не является исключением и движется вокруг Солнца, соответствуя всем трём теориям, как и все остальные планеты в Солнечной системе.
А Вы смотрели: Вращается ли Солнце вокруг своей оси?
Источник
Законы движения планет вокруг Солнца
Сначала Кеплер установил, что планеты движутся вокруг Солнца по эллипсам и Солнце находится в одном из фокусов. Эллипс — это кривая, о которой знают все художники, потому что она представляет собой растянутый круг. Дети тоже знают о нем: им рассказывали, что если продеть в кольцо бечевку, закрепить ее концы и вставить в кольцо карандаш, то он опишет эллипс.
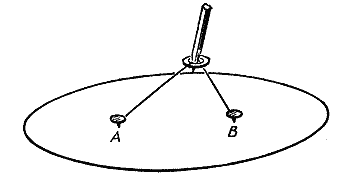
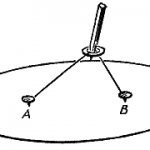
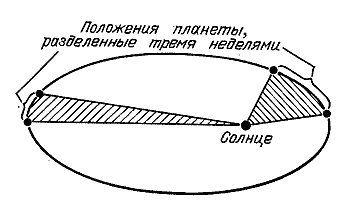
Две точки А и В — фокусы. Орбита планеты — эллипс. Солнце находится в одном из фокусов. Возникает другой вопрос: как движется планета по эллипсу? Идет ли она быстрее, когда находится ближе к Солнцу? Замедляет ли движение, удаляясь от него? Кеплер ответил и на этот вопрос. Он обнаружил, что если взять два положения планеты разделенных друг от друга определенным промежутком времени, скажем тремя неделями, потом взять другую часть орбиты и там — тоже два положения планеты разделенные тремя неделями, и провести линии (ученые называют их радиус-векторами) от Солнца к планете, то площадь заключенная между орбитой планеты и парой линий которые отделены друг от друга тремя неделями всюду одинакова, в любой части орбиты. А чтобы эти площади были одинаковы, планета должна идти быстрее, когда она ближе к Солнцу, и медленнее, когда она далеко от него.

Еще через несколько лет Кеплер сформулировал третье правило, которое касалось, не движения одной планеты вокруг Солнца, а связывало движения различных планет друг с другом. Оно гласило, что время полного оборота планеты вокруг Солнца зависит от величины орбиты и пропорциорционально квадратному корню из куба этой величины. А величиной орбиты считается диаметр, пересекающий самое широкое место эллипса.
Так Кеплер открыл три закона, которые можно свести в один, если сказать, что орбита планеты представляет собой эллипс — за равные промежутки времени радиус-вектор планеты описывает равные площади и время (период) обращения планеты вокруг Солнца пропорционально величине орбиты в степени три вторых, т. е. квадратному корню из куба величины орбиты. Эти три закона Кеплера полностью описывают движение планет вокруг Солнца.
Тем временем Галилей открыл великий принцип инерции
. Затем наступила очередь Ньютона, который решил, что планете, вращающейся вокруг Солнца, не нужна сила, чтобы двигаться вперед; если бы никакой силы не было, планета летела бы по касательной. Но на самом деле планета летит не по прямой. Она все время оказывается не в том месте, куда попала бы, если бы летела свободно, а ближе к Солнцу. Другими словами, ее скорость, ее движение отклоняются в сторону Солнца.
Стало ясно, что источник этой силы (силы притяжения) находится где-то около Солнца.
Люди рассматривали в телескоп Юпитер со спутниками, обращающимися вокруг него, и им это напоминало маленькую Солнечную систему. Все выглядело так, будто спутники притягиваются к Юпитеру. Луна тоже вращается вокруг Земли и притягивается к ней точно таким же образом. Естественно, возникла мысль, что притяжение действует повсюду. Оставалось лишь обобщить эти наблюдения и сказать, что все тела притягивают друг друга. А значит, Земля должна притягивать Луну так же, как Солнце притягивает планеты. Но известно, что Земля притягивает и обычные предметы: вы, например, прочно сидите на стуле, хотя вам, может быть, и хотелось бы летать по воздуху. Тяготение предметов к Земле было явлением, хорошо известным. Ньютон предположил, что Луну на орбите удерживают те же силы, которые притягивают предметы к Земле.
Учебник. Законы Кеплера
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
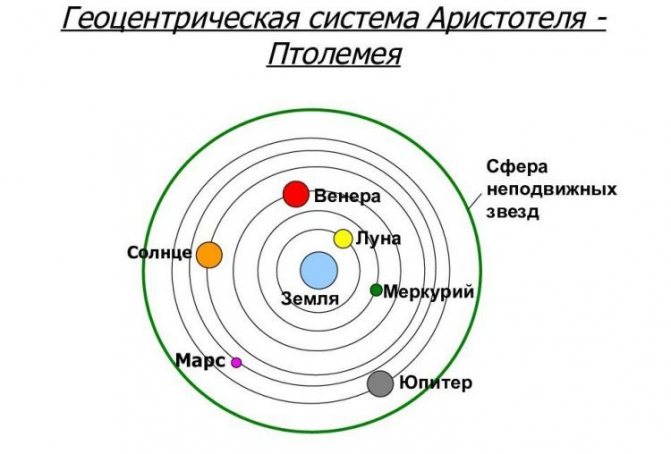
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (~ 140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
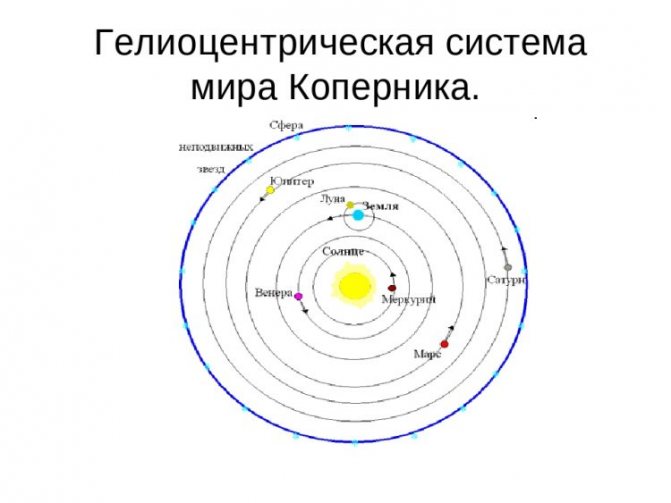
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном И. Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Т. Браге.
Первый закон Кеплера (1609 г.):
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P
траектории называется перигелием, точка
A
, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.
Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым.
Второй закон Кеплера (1609 г.):
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Рис. 1.24.3 иллюстрирует 2-й закон Кеплера.
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела p → и его составляющие p → r и p → ⊥ . Площадь, заметенная радиус-вектором за малое время Δt
, приближенно равна площади треугольника с основанием
rΔθ
и высотой
r
: Δ S = 1 2 r 2 Δ θ или Δ S Δ t = 1 2 r 2 Δ θ Δ t = 1 2 r 2 ω ; ( Δ t → 0 ) .
Здесь ω = Δ θ Δ t ; ( Δ t → 0 ) – угловая скорость (см. §1.6).
Момент импульса L
по абсолютной величине равен произведению модулей векторов p → ⊥ и r → :
L = r p ⊥ = r ( m υ ⊥ ) = m r 2 ω , так как υ ⊥ = r ω .
Из этих отношений следует: Δ S Δ t = L 2 m ; ( Δ t → 0 ) .
Поэтому, если по второму закону Кеплера Δ S Δ t = const, то и момент импульса L
при движении остается неизменным.
В частности, поскольку скорости планеты в перигелии υ → P и афелии υ → A направлены перпендикулярно радиус-векторам r → P и r → A , из закона сохранения момента импульса следует: rPυP = rAυA
.
Третий закон Кеплера (1619 г.):
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:
T 2 a 3 = const или T 1 2 a 1 3 = T 2 2 a 2 3 .
Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 %
.
На рис. 1.24.4 изображены две орбиты, одна из которых – круговая с радиусом R
, а другая – эллиптическая с большой полуосью
a
. Третий закон утверждает, что если
R = a
, то периоды обращения тел по этим орбитам одинаковы.
Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения: F = G M m r 2 , где M
и
m
– массы Солнца и планеты,
r
– расстояние между ними,
G = 6,67ċ10–11 Нċм2/кг2
– гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, уже говорилось, что сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу.
Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T2 ~ R3
, где
Т
– период обращения,
R
– радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца: F ~ ω 2 R = ( 2 π ) 2 R T 2 .
Если T2 ~ R3
, то F ~ 1 R 2 .
Свойство консервативности гравитационных сил (см. §1.10) позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.
Потенциальная энергия тела массы m
, находящегося на расстоянии
r
от неподвижного тела массы
M
, равна работе гравитационных сил при перемещении массы
m
из данной точки в бесконечность.
Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа Δ A i гравитационной силы F → на малом перемещении Δ s → i = Δ r → i есть: Δ A i = — G M m r i 2 Δ r i .
Полная работа при перемещении тела массой m
из начального положения в бесконечность находится суммированием работ
ΔAi
на малых перемещениях: A r ∞ = ∑ r ∞ Δ A i .
В пределе при Δri → 0
эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение E p = A r ∞ = — G M m r .
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.
Если тело находится в гравитационном поле на некотором расстоянии r
от центра тяготения и имеет некоторую скорость
υ
, его полная механическая энергия равна E = E k + E P = m υ 2 2 — G M m r = const.
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6).
При E = E1 < 0
тело не может удалиться от центра притяжения на расстояние
r > rmax
. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).
При E = E2 = 0
тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории.
При E = E3 > 0
движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.
Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.
Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.
m υ 1 2 R З = G M m R З 2 = g m , отсюда υ 1 = G M R З = g R З = 7,9 ċ 10 3 м/с.
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
E = m υ 2 2 2 — G M m R З = 0, отсюда υ 2 = 2 G M R З = 2 g R З = 11,2 ċ 10 3 м / с.
Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9ċ103 м/с
и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих
υ1
, но меньших
υ2 = 11,2ċ103 м/с
, орбита корабля будет эллиптической. При начальной скорости
υ2
корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.
Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд Эллиптическая орбита планеты массой m << M
.
a
– длина большой полуоси,
F
и
F’
– фокусы орбиты Закон площадей – второй закон Кеплера Круговая и эллиптическая орбиты. При
R = a
периоды обращения тел по этим орбитам одинаковы Законы Кеплера Вычисление потенциальной энергии тела в гравитационном поле Диаграмма энергий тела массой
m
в гравитационном поле, создаваемом сферически симметричным телом массой
M
и радиусом
R
Космические скорости. Указаны скорости вблизи поверхности Земли. 1:
υ = υ1
– круговая траектория; 2:
υ1 <� υ <� υ2
– эллиптическая траектория; 3:
υ = 11,1ċ103 м/с
– сильно вытянутый эллипс; 4:
υ = υ2
– параболическая траектория; 5:
υ > υ2
– гиперболическая траектория; 6: траектория Луны
Почему происходят приливы
Во-первых, приливы. Приливы вызваны тем, что Луна сама притягивает Землю и ее океаны. Так думали раньше, но вот что оказалось необъяснимым: если Луна притягивает воды и поднимает их над ближней стороной Земли, то за сутки происходил бы лишь один прилив — прямо под Луной. На самом же деле, как мы знаем, приливы повторяются примерно через 12 часов, т. е. два раза в сутки. Была и другая школа, которая придерживалась противоположных взглядов. Ее приверженцы считали, что Луна притягивает Землю, а вода за ней не успевает. Ньютон первым понял, что происходит на самом деле: притяжение Луны одинаково действует на Землю и на воду, если они одинаково удалены. Но вода в точке у ближе к Луне, чем Земля, а в точке х — дальше. В у вода притягивается к Луне сильнее, чем Земля, а в х — слабее. Поэтому получается комбинация двух предыдущих картинок, которая и дает двойной прилив.
Фактически Земля делает то же самое, что и Луна — она движется по кругу. Сила, с которой Луна действует на Землю, уравновешивается — но чем? Как Луна ходит по кругу, чтобы уравновесить притяжение Земли, точно так же ходит по кругу и Земля. Обе они обращаются вокруг общего центра, и силы на Земле уравновешены так, что вода в х притягивается Луной слабее, в у — сильнее и в обоих местах вода вспучивается. Так были объяснены приливы и почему они происходят дважды в сутки.
Открытие скорости света
С развитием науки измерения производились все точнее и подтверждения ньютоновских законов становились все более убедительными. Первые точные измерения касались спутников Юпитера. Казалось бы, если тщательно наблюдать за их обращением, то можно убедиться, что все происходит согласно Ньютону. Однако выяснилось, что это не так. Спутники Юпитера появлялись в расчетных точках то на 8 мин раньше, то на 8 мин позже, чем полагалось бы согласно законам Ньютона. Обнаружилось, что они опережают график, когда Юпитер сближается с Землей, и отстают, когда Юпитер и Земля расходятся, — очень странное явление.
Рёмер (Олаф Рёмер (1644-1710) — датский астроном)
, убежденный в правильности закона тяготения, пришел к интересному выводу, что для путешествия от спутников Юпитера до Земли свету требуется определенное время, и, глядя на спутники Юпитера, мы видим их не там, где они находятся сейчас, а там, где они были несколько минут назад — столько минут, сколько требуется свету, чтобы дойти до нас. Когда Юпитер ближе к нам, свет приходит быстрее, а когда Юпитер дальше — свет идет дольше; поэтому Рёмеру пришлось внести поправку в наблюдения на эту разницу во времени, т.е. учесть, что иногда мы делаем эти наблюдения раньше, а иногда позже. Отсюда ему удалось определить скорость света. Так было впервые установлено, что свет распространяется не мгновенно
Тайны вселенной
Законы движения планет
Планеты благодаря своим внешне сложным движениям сыграли решающую роль в астрономии и вообще в построении фундамента механики и физики. Еще древнегреческие астрономы поставили вопрос, не являются ли наблюдаемые сложные перемещения по небу лишь отражением более регулярных движений планет в пространстве. С этого времени начинается теоретическое построение схем планетной системы, или же, как мы говорили выше, кинематики планетных движений в пространстве.
Один из первых коперниканцев, немецкий математик и астроном Эразм Рейнгольд (1511—1553) составил в 1551 году, основываясь на гелиоцентрической системе Коперника, таблицы движения планет, названные им «Прусские таблицы». Эти таблицы оказались более точными, чем все предыдущие, основанные на старых схемах, и это очень способствовало укреплению идеи гелиоцентризма, с огромным трудом пробивающей себе путь сквозь устоявшиеся веками и привычные для тех времен взгляды, а также преодолевающей реакционное идеологическое давление церкви.
Тем не менее вскоре астрономы обнаружили расхождение и этих таблиц с данными наблюдений движения небесных тел.
Для передовых ученых было ясно, что учение Коперника правильно, но надо было глубже исследовать и выяснить законы движения планет. Эту задачу решил великий немецкий ученый Кеплер.
Иоганн Кеплер (1571—1630) появился на свет в маленьком городке Вейле близ Штутгарта. Кеплер родился в бедной семье, и поэтому ему с большим трудом удалось окончить школу и поступить в 1589 году в Тюбингенский университет Здесь он с увлечением занимался математикой и астрономией. Его учитель профессор Местлин втайне был последователем Коперника. Конечно, в университете Местлин преподавал астрономию по Птолемею, но дома он знакомил своего ученика с основами нового учения. И вскоре Кеплер стал горячим и убежденным сторонником теории Коперника.
В отличие от Местлина, Кеплер не скрывал своих взглядов и убеждений. Открытая пропаганда учения Коперника очень скоро навлекла на него ненависть местных богословов. Еще до окончания университета, в 1594 году, Иоганна посылают преподавать математику в протестантское училище города Граца, столицы австрийской провинции Штирии.
Уже в 1596 году он издает «Космографическую тайну», где, принимая вывод Коперника о центральном положении Солнца в планетной системе, пытается найти связь между расстояниями планетных орбит и радиусами сфер, в которые в определенном порядке вписаны и вокруг которых описаны правильные многогранники. Несмотря на то что этот труд Кеплера оставался еще образцом схоластического, квазинаучного мудрствования, он принес автору известность Знаменитый датский астроном-наблюдатель Тихо Браге (1546—1601), скептически отнесшийся к самой схеме, отдал должное самостоятельности мышления молодого ученого, знанию им астрономии, искусству и настойчивости в вычислениях и выразил желание встретиться с ним. Состоявшаяся позже встреча имела исключительное значение для дальнейшего развития астрономии.
В 1600 году приехавший в Прагу Браге предложил Иоганну работу в качестве своего помощника для наблюдений неба и астрономических вычислений. Незадолго перед этим Браге был вынужден оставить свою родину Данию и выстроенную им там обсерваторию, где он в течение четверти века вел астрономические наблюдения. Эта обсерватория была снабжена лучшими измерительными инструментами, а сам Браге был искуснейшим наблюдателем. Ученый с большим интересом относился к учению Коперника, но сторонником его не был. Он выдвигал свое объяснение устройства мира: планеты он признавал спутниками Солнца, а Солнце, Луну и звезды считал телами, обращающимися вокруг Земли, за которой, таким образом, сохранялось положение центра всей Вселенной.
Браге работал вместе с Кеплером недолго: в 1601 году он умер. После его смерти Кеплер начал изучать оставшиеся материалы с данными долголетних астрономических наблюдений. Работая над ними, в особенности над материалами о движении Марса, Кеплер сделал замечательное открытие: он вывел законы движения планет, ставшие основой теоретической астрономии.
Отправным пунктом для Кеплера служило сравнение теории и наблюдений. Дело в том, что к концу XVI века Прусские таблицы, составленные, как уже говорилось выше, стали предсказывать движение планет очень неточно Наблюденные и вычисленные по этим таблицам положения планет отличались на 4—5 градусов, что было недопустимо в астрономической практике. Отсюда вытекало, что планетная теория Коперника нуждается в исправлении и дополнении.
В начале Кеплер пошел по пути уточнения и усложнения схемы Коперника. Конечно, он был глубоко убежден в истинности принципа гелиоцентризма и стал подбирать новые комбинации окружностей (эпициклов, эксцентров). Ему удалось подобрать, в конце концов, такую комбинацию, что его схема давала ошибку по сравнению с наблюдениями до 8 минут. Но Кеплер был уверен, что Тихо Браге в своих наблюдениях не мог допускать таких ошибок.
Поэтому Кеплер заключил, что «виновата» теория, поскольку она не согласуется с астрономической практикой. Он отбросил полностью схему, основанную на эпициклах и эксцентрах, и стал искать другие схемы.
Кеплер пришел к мысли о неправильности установившегося с древности мнения о круговой форме планетных орбит. Путем вычислений он доказал, что планеты движутся не по кругам, а по эллипсам — замкнутым кривым, форма которых несколько отличается от круга. При решении данной задачи Кеплеру пришлось встретиться со случаем, который, вообще говоря, методами математики постоянных величин решен быть не мог. Дело сводилось к вычислению площади сектора эксцентрического круга. Если эту задачу перевести на современный математический язык, мы придем к эллиптическому интегралу. Дать решение задачи в квадратурах Кеплер, естественно, не мог, но он не отступил перед возникшими трудностями и решил задачу путем суммирования бесконечно большого числа «актуализированных» бесконечно малых. Этот подход к решению важной и сложной практической задачи представлял собой в новое время первый шаг в предыстории математического анализа.
Первый закон Кеплера предполагает, что Солнце находится не в центре эллипса, а в особой точке, называемой фокусом. Из этого следует, что расстояние планеты от Солнца не всегда одинаковое. Так как эллипс — плоская фигура, то первый закон подразумевает, что каждая планета движется, оставаясь все время в одной и той же плоскости.
Второй закон звучит так: радиус-вектор планеты (т. е. отрезок, соединяющий Солнце и планету) описывает равные площади в равные промежутки времени. Этот закон часто называют законом площадей. Второй закон указывает, прежде всего, на изменение скорости движения планеты по ее орбите: чем ближе планета подходит к Солнцу, тем быстрее она движется. Но этот закон дает на самом деле больше. Он целиком определяет движение планеты по ее эллиптической орбите.
Оба закона Кеплера стали достоянием науки с 1609 года, когда была опубликована его знаменитая «Новая астрономия» — изложение основ новой небесной механики. Однако выход этого замечательного произведения не сразу привлек к себе должное внимание: даже великий Галилей, по-видимому, до конца дней своих так и не воспринял законов Кеплера.
Кеплер интуитивно чувствовал, что существуют закономерности, связывающие всю планетную систему в целом. И он ищет эти закономерности в течение десяти лет, прошедших после публикации «Новой астрономии». Богатейшая фантазия и огромное усердие привели Кеплера к его так называемому третьему закону, который, как и первые два, играет важнейшую роль в астрономии. Кеплер издает «Гармонию мира», где он формулирует третий закон планетных движений. Ученый установил строгую зависимость между временем обращения планет и их расстоянием от Солнца. Оказалось, что квадраты периодов обращения любых двух планет вокруг солнца относятся между собой как кубы их средних расстояний от Солнца. Это — третий закон Кеплера.
«Третий закон Кеплера играет ключевую роль при определении масс планет и спутников, — пишут в своей книге Е.А. Гребенников и Ю.А. Рябов. — Действительно, периоды обращения планет вокруг Солнца и их гелиоцентрические расстояния определяются с помощью специальных математических методов обработки наблюдений, а массы планет непосредственно из наблюдений невозможно получить. В нашем распоряжении нет грандиозных космических весов, на одну чашу которых мы положили бы Солнце, а на другую — планеты. Третий закон Кеплера и компенсирует отсутствие таких космических весов, так как с его помощью мы легко можем определить массы небесных тел, образующих единую систему».
Законы Кеплера замечательны и тем, что они, если можно так выразиться, более точны, чем сама действительность. Они представляют собой точные математические законы движения для идеализированной «Солнечной системы», в которой планеты — материальные точки бесконечно малой массы по сравнению с «Солнцем». В действительности же планеты имеют ощутимую массу, так что в фактическом их движении имеются отклонения от законов Кеплера. Такая ситуация имеет место быть в случае многих известных сейчас физических законов.
Сегодня можно сказать, что законы Кеплера точно описывают движение планеты в рамках задачи двух тел, а наша Солнечная система является многопланетной системой, поэтому для нее эти законы являются лишь приближенными. Парадоксальным является к тому же тот факт, что именно для Марса, наблюдения которого и привели к их открытию, законы Кеплера выполняются менее точно.
Работы Кеплера над созданием небесной механики сыграли важнейшую роль в утверждении и развитии учения Коперника. Им была подготовлена почва и для последующих исследований, в частности для открытия Ньютоном закона всемирного тяготения. Законы Кеплера и сейчас сохраняют свое значение: научившись учитывать взаимодействие небесных тел, ученые их используют не только для расчета движений естественных небесных тел, но, что особенно важно, и искусственных, таких, как космические корабли, свидетелями появления и совершенствования которых является наше поколение.
Открытие планеты
Возникла еще одна проблема: планеты не должны двигаться по эллипсам, потому что, согласно законам Ньютона, они не только притягиваются Солнцем, но и притягивают друг друга — слабо, но все же притягивают, и это слегка изменяет их движение. Уже были известны большие планеты — Юпитер, Сатурн, Уран — и было подсчитано, насколько они должны отклоняться от своих совершенных кеплеровских орбит-эллипсов за счет взаимного притяжения. Когда эти расчеты были закончены и проверены наблюдениями, обнаружилось, что Юпитер и Сатурн движутся в полном согласии с расчетами, а с Ураном творится что-то странное. Казалось бы, еще повод усомниться в законах Ньютона; но главное — не падать духом! Два человека, Джон Кауч Адаме (1819-1892) — английский математик и астроном; Урбен Леверье (1811-1877)-французский астроном
, которые выполнили эти расчеты независимо друг от друга и почти одновременно, предположили, что на движение Урана влияет невидимая планета. Они послали письма в обсерватории с предложением: «Направьте ваш телескоп туда-то и вы увидите неизвестную планету». «Что за чепуха,- сказали в одной из обсерваторий,- какому-то мальчишке попала в руки бумага и карандаш, и он указывает нам, где искать новую планету». В другой обсерватории дирекция была легче на подъем — и там открыли Нептун!
Контрольная работа по астрономии за 1 полугодие
Контрольная работа по астрономии за 1 полугодие
I вариант
1 часть
1. Перед вами названия планет Солнечной системы:
1. Венера 2. Юпитер 3. Марс 4. Меркурий
Расположите планеты в порядке их удаления от Солнца
2. Выберите среди них планеты земной группы:
3. Планеты вращаются вокруг своей оси с запада на восток (прямое вращение). Назовите планету земной группы, имеющую обратное вращение.
1. Венера 2. Марс 3. Юпитер 4. Уран
4. Назовите планету, не имеющую атмосферы:
1. Земля 2. Юпитер 3. Меркурий 4. Уран
5. В составе Солнечной системы есть пояс астероидов. Между орбитами каких планет он находится?
1. Юпитера и Марса 2. Марса и Земли 3. Меркурия и Венеры
6. Особенностями планет-гигантов являются:
1. наличие атмосферы 2. отсутствие атмосферы 3. кратеры 4. наличие твердой поверхности 5. наличие спутников
7. Найдите фамилии ученых, занимавшихся изучением системы Мира.
1. Клавдий Птолемей 2. Иоганн Кеплер 3. Джордано Бруно 4. А.П.Королев
8. Из ученых выберите, кто открыл и доказал Законы движения небесных тел.
1. Николай Коперник 2. И.Кеплер 3. Г.Галилей
9. Известно, что орбита любой планеты представляет собой эллипс, в одном из фокусов которого находится Солнце. Ближайшая к Солнцу точка орбиты называется:
1. апогей 2. перигей 3. афелий 4. перигелий
10.Формулой T12(M0+m1) = a13 выражается:
T22(M0+m2) a23
1. Первый закон Кеплера 2. Второй закон Кеплера 3. Третий закон Кеплера 4. Третий закон Ньютона
11. В основе определения радиуса Земли лежат измерения линейного и углового расстояния между двумя точками поверхности, расположенными на одном меридиане. Угловое расстояние – это:
1. разность географической долготы точек 2. разность географической широты 3. горизонтальный параллакс светила 4. разница поясного времени
12. Соотнесите понятия (А — Д) и определения
1. высота полюса мира над горизонтом 2. числа, с помощью которых указывают положение точки на поверхности 3. линия, соединяющая полюса и проходящая через заданную точку
А) Координаты Б) Широта В) Долгота Г) Параллели Д) Меридианы
13. Соотнесите понятия (А — Д) и определения:
1. момент верхней кульминации Солнца 2. промежуток времени между двумя прохождениями Солнца через точку равноденствия 3. постоянная единица времени
А) Секунда Б) Сутки В) Год Г) Полдень Д) Полночь
14. Соотнесите понятия (А — Д) и определения:
1. время на гринвичском меридиане 2. единое условное время между двумя меридианами с расстоянием в 15° 3. перевод времени на 1 час назад по сравнению с поясным
А) Всемирное время Б) Поясное время В) Московское время Г) Летнее время Д) Декретное
15. Созвездие – это:
1. Группа звезд 2. Область неба 3. характерные фигуры, образуемые яркими звездами 4. участки, на которые разделена небесная сфера
2 часть
Задача 1
Каково склонение звезды, если она кульминирует на высоте 63° в Красноярске, географическая широта которого равна 56° с.ш.?
Используя соотношение, h = δ + (90° – φ):
Задача 2
Когда в Гринвиче 10 ч 17 мин 14 с, в некотором пункте местное время равно 12 ч 43 мин 21 с. Какова долгота этого пункта?
3 часть
Объясните различие систем мира геоцентрической и гелиоцентрической.
II вариант
1 часть
1. Перед вами названия планет Солнечной системы:
1. Сатурн 2. Юпитер 3. Марс 4. Земля
Расположите планеты в порядке их удаления от Солнца
2. Выберите среди них планеты земной группы:
3. Планеты вращаются вокруг своей оси с запада на восток (прямое вращение). Назовите планету земной группы, имеющую обратное вращение.
1. Венера 2. Марс 3. Земля 4. Уран
4. Назовите планету, не имеющую атмосферы:
1. Земля 2. Юпитер 3. Меркурий 4. Сатурн
5. В составе Солнечной системы есть метероиды. К каким объектам они относятся:
1. малые тела 2. космическая пыль 3. промежуточное место между астероидами и пылью
6. Особенностями планет земной группы являются:
1. наличие атмосферы 2. высокая температура поверхности 3. кратеры 4. наличие твердой поверхности 5. наличие спутников
7. Найдите фамилии ученых, занимавшихся изучением системы Мира.
1. М.В.Ломоносов 2. Иоганн Кеплер 3. Джордано Бруно 4. А.П.Королев
8. Из ученых выберите, кто доказал Законы движения небесных тел.
1. Николай Коперник 2. И.Кеплер 3. Г.Галилей 4. Тихо Браге
9. Известно, что орбита любой планеты представляет собой эллипс, в одном из фокусов которого находится Солнце. Наиболее удаленная от Солнца точка орбиты называется:
1. апогей 2. Перигей 3. Афелий 4. Перигелий
10. Формулой T12(M0+m1) = a13 выражается:
T22(M0+m2) a23
1. Первый закон Кеплера 2. Второй закон Ньтона 3. Третий закон Кеплера 4. Третий закон Ньютона
11. В основе определения радиуса Земли лежат измерения линейного и углового расстояния между двумя точками поверхности, расположенными на одном меридиане. Угловое расстояние – это:
1. разность географической долготы точек 2. разность географической широты 3. горизонтальный параллакс светила 4. разница поясного времени
12. Соотнесите понятия (А – Д) и определения
1. высота полюса мира над горизонтом 2. числа, с помощью которых указывают положение точки на поверхности 3. линия, соединяющая полюса и проходящая через заданную точку
А) Координаты Б) Широта В) Долгота Г) Параллели Д) Меридианы
13. Соотнесите понятия (А – Д) и определения:
1. момент верхней кульминации Солнца 2. промежуток времени между двумя прохождениями Солнца через точку равноденствия 3. постоянная единица времени
А) Секунда Б) Сутки В) Год Г) Полдень Д) Полночь Г) Час
14. Соотнесите понятия (А – Д) и определения:
1. время на гринвичском меридиане 2. единое условное время между двумя меридианами с расстоянием в 15° 3. перевод времени на 1 час назад по сравнению с поясным
А) Всемирное время Б) Поясное время В) Московское время Г) Зимнее Д) Декретное
15. Небесная сфера- это:
1. часть Вселенной 2. Математическая модель небосвода 3. воображаемая сфера произвольного радиуса, на которую проецируются небесные тела.
2 часть
Задача 1
Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
Задача 2
Переведите в часовую меру долготу Красноярска (l=92°52/ в.д.).
3 часть
Объясните современную систему отсчета времени (календарь)